Satellite based quantum cryptography

Cryptography is, beyond any doubt, an important technology. Keeping the privacy of communications has many applications in modern societies. For instance, being able to send a message, as your credit card number, with the confidence that no one will understand it if it is intercepted, is a basic assumption for electronic transactions. Also, nowadays and in the past, military services use cryptography for avoiding the enemy to realize their plans.
Typical cryptographic methods are based in mathematical complexity. If you use a password as long as the message, and you use it only once, you can assure that the encrypted message is indecipherable. This method is called the one-time pad. The problem then is to send the password, because if you have a secure channel for it, you could also send the message itself. Another, most used, method is public-key cryptography. This one is based in mathematical operations, as integer factorization, that are very easy to compute in one direction, but very difficult in the other one. The security of this method relies in two basic assumptions, that the eavesdropper who wants to decode the message has a limited computing power, and that she has not developed a faster algorithm to decoding compared with the state of the art.
Quantum cryptography 1 represents a very different approach to this problem. Instead of creating a problem very expensive to solve, measuring this expensiveness by the computing time, it is based on the quantum properties of particles. Due to this it is unbreakable in the limit of perfect communication, and very difficult to break for more realistic scenarios. The basic idea is simple. Alice wants to send a secret message to Bob but she knows that there is an eavesdropper, Eve, who wants to read it. Hence, she can codify the message by the use of a one-type pad. The message can be send by any usual (classical) channel, as it can only be decoded if the password is known. The problem now is how to send the password itself to Bob. In order to perform that she encodes a random password in the polarization state of single photons. She can choose to polarize these photons in two different ways, which only she knows, and each choice corresponds to a bit of the password. Furthermore, if Eve intercepts it, she can only measure the polarization of each photon in one of the basis, but she does not know which one was used by Alice. Due to the quantum properties of photons, if Eve measures the photons in a basis different to the one used by Alice, she changes the state. That will happen in mean for half of the photons. When Bob receive the password he measures them, again randomly. Then Alice and Bob can share the basis they used and for the cases when they measure the same they should obtain the same result, that is again half of the photons. This information can be share by a non-secure channel, as they do not care if anyone is eavesdropping. If Eve has intercept the communication, Alice and Bob can realize that they do not obtain the same result, and the communication can be cancelled. That is revolutionary for two reasons. First, it does not depend on the computation abilities of Eve. Second, they can even know if someone is spying on them, something almost impossible with computational cryptography.
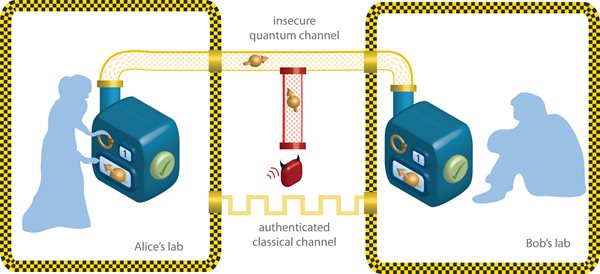
Unfortunately, the problem has not been completely solved for practical purposes. Quantum cryptography is unbreakable only in the limit of perfect communications, when Bob and Alice can be sure that they will receive the same state if there is not eavesdropping. In real world, most of the quantum channels have losses, changes of the state due to the interaction of the photons with the environment. These interactions can mimic the effect of Eve, and detecting how many changes are acceptable is highly non trivial.
One thing is then sure, for having robust and useful quantum cryptography there is need of sending a high number of photons for long distances with a minimum number of loses. This is the purpose of two recent experimental papers.
The Tenerife Experiment
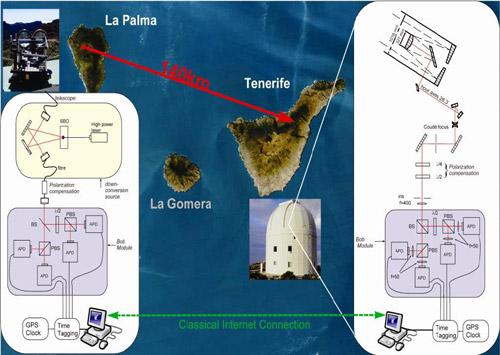
Several experiments have been performed in Tenerife during last years, principally promoted by the research group of Anton Zeilinger 2. The principal purpose of these experiments was to send quantum information for long distances. For performing this task they choose two islands, La Palma and Tenerife, separated by 144 km. This distance is considered enough to simulate the transmission between a ground base and a geostationary satellite. The experimental setup is displayed in Figure 2. By analyzing the statistics of the received and sent photons the authors concluded that they were able to obtain a secure key rate of 42 bit/s. That means that after discarding the photons that were deteriorated during the transmission they were able to transmit 42 bits per second with a high probability of no eavesdropping.
Munich Experiment
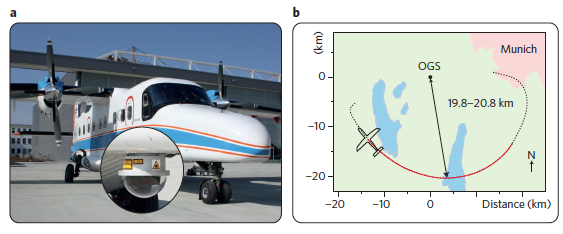
Even if the distance of the Tenerife experiment can be equivalent, once the difference of densities of the atmosphere is taken into account, to the transmission of information from a ground base and a satellite, one important part was still missing. The principal concern about the relevance of this experiment to satellite based communications is the following: In this experiment both the emisor and the receiver where static, but satellites are not. The problem then is to send quantum information from a ground base to a rapidly moving receptor, and the other way around. This is the problem treated in Reference 3.
In this experiment the signal was send by a Dornier 228 turboprop aircraft operated by the German Aerospace Center to a ground center. This aeroplane was moving at 290 km/h, with a mean distance of 20 km to the base. The experiment was performed during the new moon and other possible contamination sources, as the anticollision lights, were taken into account. Even with all this restrictions they obtained a secure key rate of 7.9 bits/s. The authors expect to improve this rate in future experiments by increasing the telescope coupling.
Even if the rates of both experiments, Tenerife and Munich, are not high compared, as instance, with the Internet transferring ratio, these two works represent a milestone in quantum communication and cryptography. First, the possibility of transferring a secure quantum key a distance equivalent to the distance to satellites has been probed. Second, the possibility of sending the same quantum information from a rapidly moving source has also been demonstrated. There are many technical problems still to be solved in order to have fast and secure quantum cryptography via satellites, but the main obstacles have already been saved.
References
- N. Gisin, G. Ribordy, W. Tittel and H. Zbinden. Quantum Cryptography. Review of Modern Physics. 74, 145 (2002) ↩
- T. Schmitt-Manderbach, H, Weier, M. Fürst, R. Ursin, F. Tiefenbacher, Th. Scheidl, J. Perdigues, Z. Sodnik, J. G. Rarity, A. Zeilinger, H. Weinfurter. Experimental Demonstration of Free-Space Decoy-State Quantum Key Distribution over 144 km. Phys. Rev. Lett. 98, 010504 (2007) ↩
- S. Nauerth, F. Moll, M. Rau, C. Fuchs, J. Horwath, S. Frick and H. Weinfurter. Air-to-ground quantum communication. Nature Photonics (2013). Doi: 10.1038/NPHOTON.2013.46 ↩