Autorotating seeds: to fly or to die

Mechanical Engineering • Physics • Plant biology • Science
By Mireia Altimira 11 comments Print

Maples rely on wind, upward currents, and gusts to spread their seeds over long distances that can reach several kilometers. Maple seeds are able to autorotate because their center of gravity, determined by the position of the nut, is located at the base of the wing-shaped seed. It has been observed that, despite their small size and slow velocities, these seeds are able to generate high lift, being able to remain in the air for longer times than other non-rotating seeds. The aerodynamic mechanisms that produce such high lift are, however, unknown. The experimental work carried out by Lentink et al. 1 on three different maple seeds (m1, m2, m3 in Fig. 1 B) and a hornbeam seed (h in Fig. 1 B) shows that the generation of a stable Leading-Edge Vortex (LEV) similar to that observed in hovering insects, bats and some birds is responsible for such high lift force.

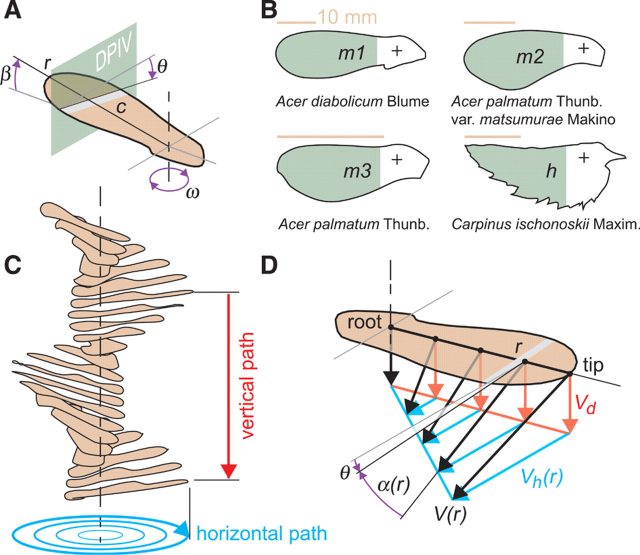
Kinematics and morphology of all four autorotating seeds studied. (A) Free-flight parameters: local wing radius, r; local chord length, c; pitch angle, θ; cone angle, β; angular velocity, ω. (B) Planform of the three maple seeds (m1, m2, m3) and hornbeam seed (h); the green area indicates the region for which DPIV around the wing was performed. + indicates the center of gravity, which corresponds closely to the center of rotation. (C) Free-flight sequence of an autorotating seed showing both the vertical (red) and horizontal, circular translation (blue) of a wing section during a full period. (D) Definition of the local geometric angle of attack and the effective aerodynamic angle of attack, α.
Kinematics and morphology of all four autorotating seeds studied. (A) Free-flight parameters: local wing radius, r; local chord length, c; pitch angle, θ; cone angle, β; angular velocity, ω. (B) Planform of the three maple seeds (m1, m2, m3) and hornbeam seed (h); the green area indicates the region for which DPIV around the wing was performed. + indicates the center of gravity, which corresponds closely to the center of rotation. (C) Free-flight sequence of an autorotating seed showing both the vertical (red) and horizontal, circular translation (blue) of a wing section during a full period. (D) Definition of the local geometric angle of attack and the effective aerodynamic angle of attack, α. | Credit : Lentink et al (2009)

Kinematics and morphology of autorotating seeds

The function of stable autorotation in maple seeds is to create lift to prolong their descent. This depends on the interaction between the inertial and aerodynamic properties of the seeds, which are not fully understood. The free-flight parameters and the shape of the studied seeds are displayed in Fig.1 A and B, respectively.

Formally, the angle of attack is defined as the angle between a body’s reference line (often the chord line) and the vector representing its relative motion respect to the oncoming flow. In the paper, the authors distinguish between the wing’s local geometric angle of attack, defined as the arctangent of descent speed, Vd, divided by horizontal speed, Vh; and the aerodynamic angle of attack, which is equal to geometric angle of attack minus the pitch angle. Even though the pitch angle is approximately constant along the span of the seed, for the study the values measured at 75% span of the four types of seed have been adopted: m1 (−1.17°), m2 (−1.39°), m3 (−0.90°), h (−2.16°).

In conventional wings and helicopter blades, the lift force increases with the angle of attack up to a critical value. An increase of the angle of attack beyond this critical point causes the air to separate from the wing, losing lift. This situation is known as stall. However, it is known that hovering insects generate very high lift even when operating at larger angles of attack, thanks to the generation of a leading-edge vortex (LEV). The main hypothesis of the paper is that this mechanism occurs also on the descent of autorotating seeds.

Leading Edge Vortex (LEV)

As mentioned above, stall occurs at high angles of attack due to flow separation, reducing the lift. In some specific wing geometries like those of insects or delta wings, separation occurs near the leading edge of the wing and the flow rolls up forming a vortex that lies on the wing surface. This vortex, commonly known as Leading Edge Vortex, increases both the lift and drag forces acting on the wing. Its structure depends on the shape of the wing, the angle of attack and the Reynolds number. The Reynolds number is a dimensionless number that gives the ratio of inertial to viscous forces in a flow (, where and stand for the density and viscosity of the fluid, respectively; and V and L for the characteristic velocity and linear dimension of the flow), and it has been estimated to be on the order of 1000 for autorotating seeds.

Large-scale experiments

To test the hypothesis of LEV generation, Lentink et al. built a dynamically scaled model. That means that both flight parameters and the Reynolds number of the model seeds were scaled such that they are identical to real seeds descending in air. Hence, for larger and faster model seeds used in the experiments, it was necessary to adopt a more viscous fluid, namely mineral oil.

Stereo digital particle image velocimetry (DPIV) was used to measure the 3D velocity field at different spanwise slices of the model seeds moving through a tank of mineral oil. This optical technique involves illuminating a plane of the flow with a laser sheet and capturing the light scattered by small seeded particles on a pair of frames. Then, the images are divided in small “interrogation areas” and a velocity vector is extracted by performing mathematical correlation analysis on a cluster of particles within each interrogation region between the two frames.

Measurements prove the generation of LEVs near the base of all the studied seeds (Fig. 2). Toward the tip, the LEV merges with the tip vortex, resulting in a trail of vorticity in the wake of the seeds. Due to the rotation of the wing, the maximum angle of attack appears at the wing root (nearly 90°), and the minimum at the wing tip (Fig. 1D). Based on prior free-flight measurements, the minimum angle of attack was obtained for the four types of seeds: m1 (16°), m2 (25°), m3 (26°) and h (28°). The difference in these angles can explain why the LEV is well attached to the wing’s surface of the three types of maple seeds, and more separated on the hornbeam seed (Fig. 2). The chordwise flow around the maple seeds reattaches behind the LEV near the trailing edge, whereas the flow around the hornbeam seed is more separated at the wing tip and fails to reattach.

Figure 2. The LEV measured for all four seeds [(A) m1, (B) m2, (C) m3, (D) h]. Streamlines calculated from the 3D velocity field measured using DPIV. The angle of attack of the seed increases from (A) to (D). Note that the seed spins clockwise.
Figure 2. The LEV measured for all four seeds [(A) m1, (B) m2, (C) m3, (D) h]. Streamlines calculated from the 3D velocity field measured using DPIV. The angle of attack of the seed increases from (A) to (D). Note that the seed spins clockwise. | Credit: Lentink et al (2009)
Real-size experiments

To validate the findings from the large-scale model, Lentink et al. built a vertical wind tunnel to study freely flying maple seeds. By matching the velocity of the flow in the tunnel with the descent rate of the seed, it was possible to film seeds spinning at a stationary height. The seeds also flew at Reynolds numbers ~ 1000. These free-flight experiments confirmed that:

  • autorotating seeds generate a stable LEV near their base, like hovering insects’ wings (Fig. 3).
  • the LEV is more compact at lower angles of attack.
  • the strong spanwise flow stretches the LEV from the base to the tip of the wing, preventing it to grow too large that it becomes unstable and separates from the surface.
Figure 3. Visualization of the LEV for free flying real-size maple seeds. The angle of attack at the wing tip is 20° (between m1 and m2).
Figure 3. Visualization of the LEV for free flying real-size maple seeds. The angle of attack at the wing tip is 20° (between m1 and m2). Credit: Lentink et al (2009)

It has been mentioned previously that the generation of an LEV increases the lift over the wing. To find out how significant this influence is, the spanwise lift distribution was calculated by integrating vorticity within each wing section. In Fig. 4A it can be seen that the lift is maximum at 40 to 60% span for maple seeds m1 and m2, whereas it is rather constant for maple seed m3 and hornbeam seed h. It was also observed that the sectional lift coefficient (Fig. 4C) reaches very high values at the 25% span location where the LEV is attached, ranging from 2 for hornbeam to almost 5 for maple seeds.

Figure 4. (A) Spanwise lift distribution. (B) Product of sectional dynamic pressure and chord length. (C) The wing’s sectional lift coefficient [(A) divided by (B)] peaks near the wing’s base (where a LEV is present) and is minimal at the tip. (D) The distribution of angle of attack with span. The high lift coefficients near the base of the wing (C) and the corresponding LEV result from the extremely high local angles of attack, well beyond 30°.
Figure 4. (A) Spanwise lift distribution. (B) Product of sectional dynamic pressure and chord length. (C) The wing’s sectional lift coefficient [(A) divided by (B)] peaks near the wing’s base (where a LEV is present) and is minimal at the tip. (D) The distribution of angle of attack with span. The high lift coefficients near the base of the wing (C) and the corresponding LEV result from the extremely high local angles of attack, well beyond 30°. | Credit: Lentink et al (2009)
In order to determine how well autorotating seeds perform respect to gliding and straying seeds, their descent times as a function of wing loading were compared (Fig. 5A). The descent time (T) is inversely proportional to the square root of wing loading (W/S, weight per unit surface area) and directly proportional to the square root of the descent factor (DF), a dimensionless number that represents the seed’s aerodynamic efficacy for a given descent speed and wing loading. The descent factor is highest for maple m1 and decreases for m2, m3, and hornbeam h, which operate at higher angle of attacks. Gliding and straying seeds achieve long descent times despite having low descent factors because of their small wing loading. Autorotating seeds have higher descent factors so, in order to achieve similar descent times, they need much greater wing loading.

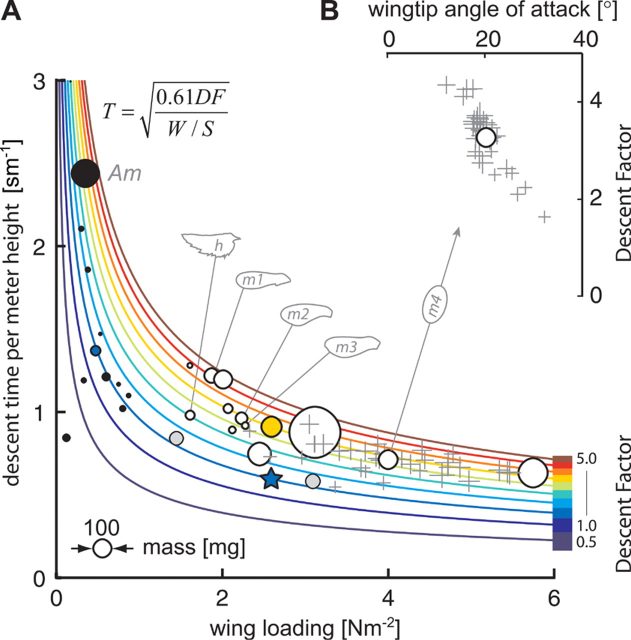
(A) Descent time of autorotating seeds (○,+) compared to gliding and straying seeds (●) as a function of wing loading, where symbol width indicates seed mass. (●) average descent time and wing loading of gliding and straying seeds. (●) average descent time and wing loading of the autorotating seeds. (★) predicted performance of gliding and straying seeds if they operated at the wing loading of autorotating seeds. (●) Ash and tulip tree seeds, which also autorotate, but spin along two major axes. (+) vertical wind tunnel measurements for maple (Acer pseudo-platanus L) seeds. Curves represent descent time as a function of wing loading at constant descent factor. Am: gliding seed Alsomitra macrocarpa, which does not rely on substantial wind for dispersal. (B) Within a population of maple seeds, descent factor increases with decreasing wing-tip angle of attack.
Figure 5. (A) Descent time of autorotating seeds (○,+) compared to gliding and straying seeds (black ●) as a function of wing loading, where symbol width indicates seed mass. (●) average descent time and wing loading of gliding and straying seeds. (Blue ●) average descent time and wing loading of the autorotating seeds. (Blue ★) predicted performance of gliding and straying seeds if they operated at the wing loading of autorotating seeds. (Gray ●) Ash and tulip tree seeds, which also autorotate, but spin along two major axes. (Gray +) vertical wind tunnel measurements for maple (Acer pseudo-platanus L) seeds. Curves represent descent time as a function of wing loading at constant descent factor. Am: gliding seed Alsomitra macrocarpa, which does not rely on substantial wind for dispersal.
(B) Within a population of maple seeds, descent factor increases with decreasing wing-tip angle of attack. | Credit: Lentink et al (2009)

Conclusions

The experiments performed by Lentink et al. show that the generation of a LEV extends the descent time of autorotating seeds, allowing them to reach further distances. The aerodynamic efficacy of these seeds increases with decreasing angle of attack, because at lower angles the LEV is more compact.

References

  1. D. Lentink, W. B. Dickson, J. L. van Leeuwen, and M. H. Dickinson, Leading-Edge Vortices Elevate Lift of Autorotating Plant Seeds, Science 324, 1438-1440 (2009) ↩

Written by

11 comments

  • Hi,

    Do you know what is the value of the torque generated during rotation of the seed around the radius of the seed?
    I am trying to find experimental data but no luck so far.

    Thank you for sharing all this information on this great web site.

    Best regards,
    Tomek

    Reply

  • Hello Tomasz,

    Thank you for your comment. In absence of wind, the only forces acting on the seed would be lift, drag and weight. Lift and weight do not generate any torque; otherwise the seed would rotate around a horizontal axis. So, you “only” need to know the drag force distribution and integrate it along the seed to get the momentum. The article does not talk about drag, it is focused on lift. However, you can look at the references of the paper for further information on experiments with maple seeds.
    Good luck with your research!
    Mireia

    Reply

  • This whole study is seriously flawed from the outset. It appears the “scientists” are not that well informed.
    ALL objects, I repeat, ALL objects moving through a fluid rotate or as they would say “auto-rotate”. In fact, It is almost not possible to stop or prevent an object from doing so. Ever heard of a little thing called “control surfaces”? these are the devices aircraft designers glue on airplanes to try to prevent them from rotating in undesired directions. They “control” the “object” moving through the fluid/air. Also, there are all sorts of fluids. Jupiter, Venus and other planets and worlds have all kinds of different fluids.
    Further examples of auto-rotation: If you drop a maple seed, airplane, car, bowlingball, house or 2×4 from 30,000 feet altitude, every single one of them will be “auto-rotating” before they hit the ground.
    Some simply entertain un-informed humans more than others.

    Reply

    • What about the realm of stable flight!!? Some bodies and shapes can stabilize at very small angles of attack although there may exist some slight coning motion or other nonplanar motion. There has been much study of circular plates descending in fluids or air and boundaries have been established between stable flight,
      rocking motion, and tumbling. I have recently studied the” ring wing” shape constructed as a thin surface made from paper. It has several stable modes of descent one of which is without any rotation at all and the axis of rotational symmetry horizontal. The length/diameter ratio has to be very small, on the order of 0.1.

      Reply

  • Hi j,

    You must be very sure of what you say because your angry and sarcastic text. Let me go through it little by little.
    – You try to discredit the authors of the original manuscript by using “scientists” with quotes. Well, you just can’t. It has been published with peer review in a top journal, so I still trust more their text than your comment.
    – ALL objects rotate (sic). True. But do they rotate in a nice and gentle spiral like maple seeds do? No. They will have aerodynamic forces that will make them move in different ways, of course. And they might also rotate at some point. But forces will be much more chaotic and the shape of your whatever-falling-object will never enable the same lift capabilities as these nicely evolved seeds. Remember that they are talking about staying more time in the air (increased lift) so seeds can be spread further.
    – Then, a nice Non Sequitur argument. Control surfaces allow to keep the plane stable. But that does not mean that when the plain is unstable it will nicely rotate; its behaviour will still be chaotic.
    – I don’t even understand why you talk about other fluids.
    – Further examples… of sarcastic comment Fail. Those objects won’t be “auto-rotating” but moving quite randomly. But you thought you could make a joke about it. Nice.
    – Actually, writing this answer entertained me quite a lot more than watching seeds fall. I might be wrong in some things I said because it is not my field, but you are plain wrong both in form and substance. Be sure that you know what you talk about when you use sarcasm and arrogance.
    Take care!

    Reply

  • Hi j,
    As Carlos says, the scientific paper from which this post is written was published in Science after a peer-review process. That means that it was sent to several researchers (all of them with a PhD degree, just like all the authors), and they judged that both method and results are scientifically correct and, therefore, publishable.
    So, don’t question the author’s work and the reviewer’s judgment without very VERY solid arguments. By doing so, you’re questioning the bases of the scientific community. Besides, sarcasm is not a good resource in a scientific discussion. When scientists talk they use facts and references to other studies to support their arguments.
    The author’s are not saying that maple seeds are the only objects in the universe that rotate when falling. They just study the aerodynamics of different seeds and report that the generation of a vortex at the leading edge of these seeds increases their lift and, therefore, the time they can stay up in the air. A longer time in the air means they can reach longer distances, which is an evolutionary advantage for plants: the more they spread, the more likely their species will thrive and survive.
    And I think you will agree with me that the way these seeds rotate is not the same as a falling house. Don’t you think it’s more like a wind turbine with one blade?

    Reply

  • Hi,
    i don’t really know that much about maple seed. My question, how many forces does maple seed have?

    Reply

    • external forces = weight forces + aerodynamic forces
      internal forces = depended to your equation of motion

      Reply

  • You may find my recent work on the the “Flight Dynamics of Samara-Type Single- Wing Autorotors” of interest under Research Gate. I also found from analysis of motion data that the span-wise flow affects the drag of a wing beyond what would be predicted from cross-flow theory. I used flight dynamics to determine the effective wing normal force coefficient and found that the dynamical motion (both drag and coning angle) can be reproduced by a constant span wise section coefficient somewhat larger than that for wings of comparable area, aspect ratio, taper, and span wise c.g. offset. I call to your
    attention that the vortices from laminar separation at the leading edge at subcritical Reynolds number are very small, and may not have been detected. These vortices are more evident is smoke tunnel photographs taken on models at these same RN. I can provide a PDF of my report if you request it. James Brunk

    Reply

  • Can these seeds in the presence of low air density, perform such flight patterns, with modifications such a larger wing span but having the same mass at the same time ?!

    Reply

Leave a Reply

Your email address will not be published.Required fields are marked *