How to create the illusion of antigravity motions

Visual illusions, a perceptual behavior where what we “see” differs from the physical reality, are used in vision science to understand the nature of human perception¹. Most of the known visual illusions come from 2D pictures and their motions, but not so many make use of 3D solid objects.

An example of the latter is the famous impossible object created by Lionel S. Penrose and Roger Penrose² showing and endless loop of stairs, known as the Penrose steps, which was used later by M.C. Escher in his artwork “Ascending and Descending”.

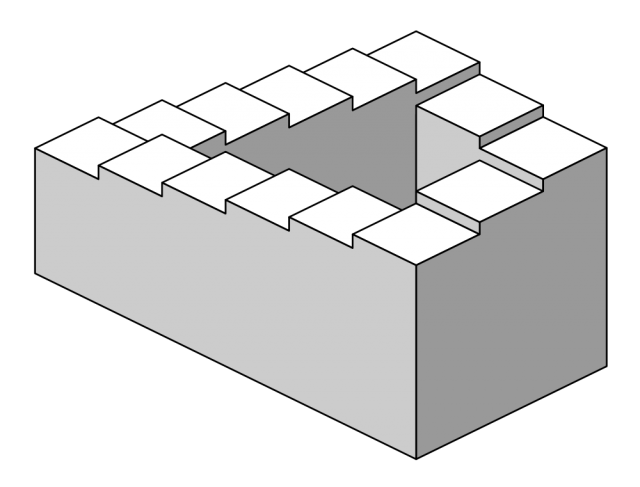
Although it is usually called an impossible object, this is not really the case. A solid structure can be constructed such that an appropriate viewpoint leads to such a picture.

Constructing this kind of structures is the aim of Sugihara³, where the author presents a method for designing solids in which the orientation of the slopes seems opposite to the actual orientation. The paper focuses in a particular type of visual illusions, called impossible motions, in which balls placed on the slopes appear to roll uphill, contradicting the law of gravity.

First, Sugihara reviews picture interpretation theory, as a tool to specify all solids represented by a given picture. For a solid object in 3D, choosing an origin for the Cartesian coordinate system determines the projection of the solid on the plane . This projection, which is the picture obtained on that plane when looking at the solid from the viewpoint at the origin, is called the line drawing of the solid.

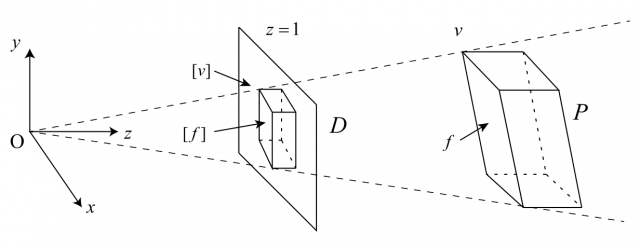
Given a solid, its line drawing is uniquely determined. But the contrary is not true: Given a line drawing, either it does not represent correctly a solid object, or there are infinitely many solids having that very same line drawing. We humans are able to interpret an ordinary line drawing as a unique solid, up to scaling. However, there might be some freedom for interpretations, which can be used to mislead human perception.

In order to do so, Sugihara takes into account the relative positions of the vertices and faces of the solid. Consider the line drawing below, in which , and are the projections of the vertices and the face of the solid.

A number of predicates stating relative positions arise from this line drawing, for example:

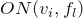• , meaning that the vertex 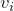is on the face .

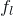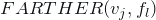• , meaning that the plane supporting 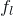passes between the viewpoint and the vertex 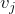(i.e., that the edge labeled is a ridge).

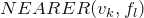• , meaning that the plane supporting 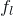passes beyond the vertex 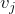(i.e., that the edge labeled is a valley).

Given a line drawing and all the predicates satisfied by the solid, how to study if the solid can be reconstructed? The answer goes through basic linear algebra.

First, observe that if a projection has coordinates , then the coordinates of the original vertex are , where is an unknown representing the multiplicative inverse of the distance between the viewpoint and (along the -axis, see again the third figure). Second, observe that the plane supporting a face has an equation , where are unknown.

Putting these two observations together, any predicate can be easily translated into linear equations and inequations. For the predicates in the previous example:

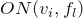• leads to .

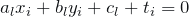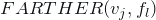• leads to .

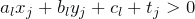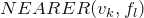• leads to .

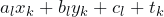In several preceding papers, Sugihara proved that a line drawing together with a set of predicates represent a 3D solid if, and only if, the corresponding system of linear equations and inequations has a solution. Hence, this system is a powerful tool to construct several 3D solids which look impossible from a certain viewpoint⁴.

However, for many structures looking impossible the system does not admit solutions at all, preventing the construction of associated 3D solids. This is the case for the so-called antigravity slopes, composed by a slope supported by two columns standing on a base plate, in which balls appear to roll uphill. In particular, from the following picture it is impossible to construct a slope that tilts to the right.

The key contribution of Sugihara is to propose a procedure to get over this issue. The idea is moving the vertices at the top of the columns, along the vertical edges of the columns, in such a way that these movements are restricted to the area covered by .

A first natural formulation is proposed but, unfortunately, it leads to a nonlinear system which is difficult to solve. Thus, Sugihara proposes a second formulation which does lead to a linear system. This allows to construct a slope as desired, which can be then combined to create more complicated constructions, causing the illusion of impossible motions.

For a last example, please enjoy the following antigravity motion illusion, which achieved the first prize in the Best Illusion of the Year Contest 2010.