The first Josephson phase-battery device

In science we try to be very precise with the wording of our texts. One of the consequences of this is that we are not afraid of repeating some words in a paragraph, or even in a sentence, if that contributes to avoid possible misunderstandings, even though it may be not recommended stylistically. Another feature of scientific communication is its abhorrence of polysemy, that is why definitions abound in any scientific text. And, as we are going to talk about a ‘phase battery’, definitions are badly needed.

If I say battery, you may think about the battery in your car, and that would be fine as an example. The battery in your car is able to produce a voltage of 12 V so that the electric devices in the car can work. But, actually, an electric battery is a number of electric cells joined together; in the case of the car battery, it usually consists of 6 cells connected in series. A battery is just a number of things of the same type joined together.

A phase could be a homogeneous part of a heterogenous system, but this is not the one we are interested now. The phase we are talking about is the stage that a periodic motion has reached, usually by comparison with another such motion of the same frequency. If we represent those periodic motions as waves, they will be in phase if their maximum and minimum values occur at the same instants; otherwise, there is said to be a phase difference.

Putting both words together, phase battery, even though we have given their definitions, still makes no sense. We need something more.

We know that quantum systems are described by sets of wave functions, mathematical expressions involving the coordinates of a particle in space, that are solutions of the Schrödinger equation. There we have our waves. Then, if a classical battery converts chemical energy into a persistent voltage bias that can power electronic circuits, a phase battery is a quantum device that provides a persistent phase bias to the wave function of a quantum circuit. Phase batteries represent a key element for quantum technologies based on phase coherence. Now, a team of researchers demonstrate ¹ a phase battery in a hybrid superconducting circuit.

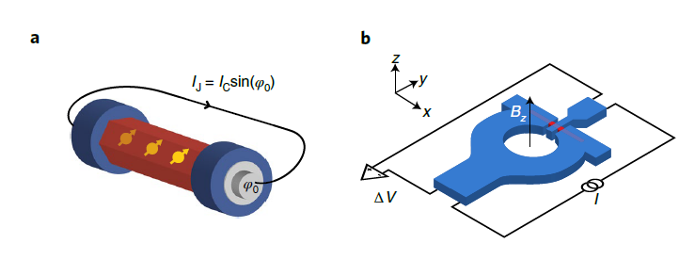
At the base of phase-coherent superconducting circuits is the Josephson effect: a quantum phenomenon describing the flow of a supercurrent in weak links between two superconductors. When we approximate two superconducting materials at low temperature, so that they are only separated by a very thin layer (less than 10 nanometres thick) of an insulating material, some new and very interesting electrical effects can be observed. First, a supercurrent, a current with zero resistance, can flow through the barrier. If this current exceeds a critical value, this conductivity is lost; the barrier then only allows the small current flow due to the tunnel effect and a voltage develops across the junction. If we apply a magnetic field below the critical current value we will find that the net current through the barrier depends on the magnetic field that we are applying. If the field increases beyond a critical value the supercurrent vanishes. A junction like the one we have just described is called a Josephson junction.

But, what if instead of an insulating material we use a conducting metal in a Josephson junction? In this case superconducting correlations are induced in the normal metal due to the proximity effect. At the interface between a normal conductor and a superconductor, charge is transferred from the normal conductor to the superconductor.

The point is that the Josephson current is intimately connected to the macroscopic phase difference between the two superconductors via the so-called current–phase relationship. The implementation of a phase battery is prevented by symmetry constraints, either time-reversal or inversion, which impose a rigidity on the superconducting phase, a universal constraint valid for any quantum phase. It follows that, if both time-reversal and inversion symmetries could be broken, a finite phase shift can be induced. A junction like this, a φ₀-junction, will generate a constant phase bias in an open circuit configuration, while when inserted into a closed superconducting loop it will induce a so-called anomalous Josephson current.

Lateral hybrid junctions made of materials with a strong spin–orbit interaction or topological insulators are ideal candidates to engineer Josephson φ₀-junctions. The new phase battery (see figure) consists of a Josephson junction made of an indium arsenide (InAs) nanowire (in red) embedded (proximitized) between two aluminium (Al) superconducting poles (in blue).

The researchers find that the ferromagnetic polarization of the unpaired-spin states is efficiently converted into a persistent phase bias across the wire, leading to the anomalous Josephson effect. The application of an external in-plane magnetic field and, thereby, achieve a continuous tuning of the phase. Or, in other words, the quantum phase battery can be charged and discharged.

This quantum element, providing a controllable and localized phase bias, can find key applications in different quantum circuits such as an energy tuner for superconducting flux and hybrid qubits, or a persistent multi-valued phase-shifter for superconducting quantum memories as well as superconducting rectifiers.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance

Disclaimer: Parts of this article may be copied verbatim or almost verbatim from the referenced research paper.