Reaching the ideal glass in polymer spheres

Common glass, used in windows or bottles, for example, is made by heating a mixture of calcium oxide (lime), sodium carbonate (soda), and silicon (IV) oxide (sand), resulting in a calcium silicate. This silicate is not a crystal but a solid in which atoms are random and have no long-range ordered pattern. These kind of solids, called “glasses”, characteristically have no definite melting point, softening over a range of temperatures instead.

A diverse class of materials, a variety of viscous liquids and colloidal suspensions, happens to solidify in a nonequilibrium state where there is no long-range order as in crystals, under conditions that are still not fully understood. This transition, which can be reversed, is not a phase transition, as it occurs over a temperature range rather than at a particular temperature. Decreasing temperature is usually the parameter triggering viscous liquids through the transition. Thus, the so-called glass transition temperature is not a clear-cut temperature (T_g) and the theory of the glass transition is much more complicated than the theory of normal phase transitions.

This is somehow related to the concept of supercooling: the cooling of a liquid to below its freezing point (which is also the melting point) without a change from the liquid to the solid state taking place. In this metastable state the particles of the liquid lose energy but do not fall into place in the lattice of the solid crystal. If the liquid is seeded with a small crystal, crystallization usually takes place and the temperature returns to the freezing point. The phenomenom is well-known and happens with waterdroplets in the atmosphere that remain unfrozen well below 0º C till something disturb them.

In general, a liquid of any kind can be cooled down below its melting temperature, provided that large cooling rates are used to avoid crystallization. Conventional supercooled liquids generally

exhibit a thermodynamic state independent of the thermal history. Further, cooling leads to the formation of a glass, whose thermodynamic state profoundly depends on the way this is formed and on its thermal history. The temperature at which the supercooled liquid loses equilibrium— which, is another way of seeing glass transition temperature, T_g—which defines the potential energy of the glass, progressively decreases with the cooling rate.

Once in the glassy state, spontaneous evolution towards low energy states takes place. Accessing these states in glasses may convey insights of utmost importance to unveil the nature of the glass transition.

W. Kauzmann noticed in 1948 that, due to its large specific heat, the entropy of a supercooled liquid decreases on cooling faster than that of the corresponding crystal. Hence, there would be a temperature, the Kauzmann temperature, T_K, at which the supercooled liquid and the crystal entropies match. But, mind you, the existence of a supercooled liquid below T_K would imply an entropy catastrophe with the paradoxical scenario of a liquid having smaller entropy than that of the

corresponding crystal. To avoid this unpalatable scenario, it has been proposed and largely debated, that a true second order thermodynamic transition, the so-called “ideal” glass transition, at T_K would take place with the emergence of an ideal glass. But, does the ideal glass exist?

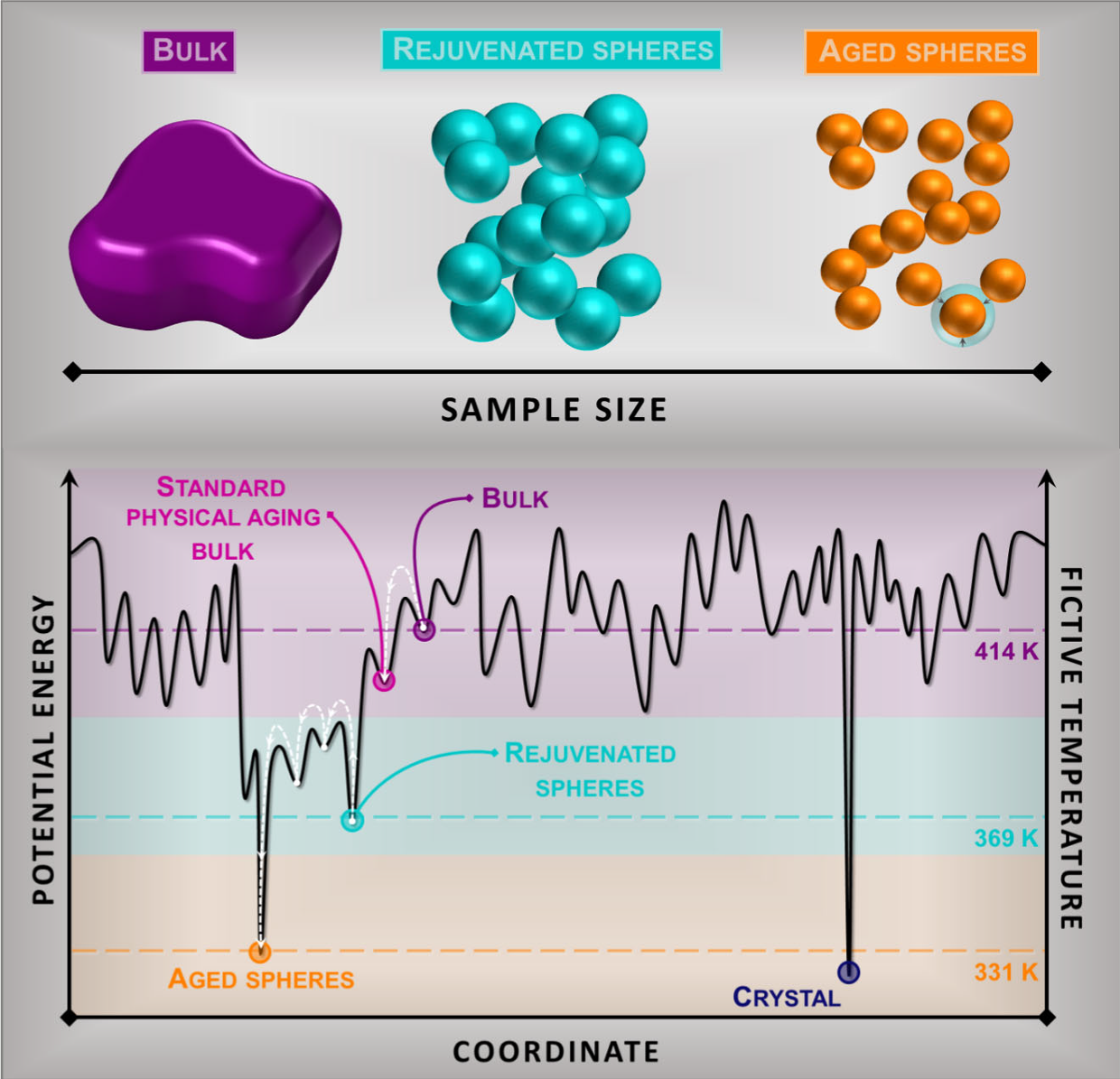
The existence of an ideal glass and the resolution to the Kauzmann paradox is a long-standing open question in materials science. Now, to address this problem, a team of researchers exploits ¹ the ability of glasses with large interfacial area to access low energy states.

Attaining information on the ideal glass transition is hampered by the transformation of the supercooled liquid into a glass. Hence, reducing the energy requires the spontaneous evolution of the glass towards the equilibrium supercooled state, a phenomenon known as physical aging. Apart from the thermodynamic view, the achievement of low energy glasses has generated intense debate on how the vibrational density of state of a glass depends on its thermodynamic state.

The researchers face these two questions submitting aggregates of spheres of a polymeric glass former, namely poly(4 − tert-butyl styrene), to aging well below their glass transition temperature, T_g. They characterize their thermodynamic state by calorimetry, and the vibrational density of states by inelastic neutron scattering.

The results show that, when aged at appropriate temperatures, glassy spheres attain a thermodynamic state corresponding to an ideal glass in time scales of about one day. The increasing glasses’ free interface induces a tremendous reduction of the timescale to recover equilibrium. In appropriate conditions via a relaxation process with finite timescale deep in the glassy state, this acceleration allows attaining glass energies relevant to detect a kink in the enthalpy, identified with the transformation from the standard into the ideal glass.

So, yes, ideal glasses exist.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance

Disclaimer: Parts of this article may be copied verbatim or almost verbatim from the referenced research paper.