Generation of net spins on chiral GNRs
Graphene nanoribbons (GNRs), are strips of graphene with ultra-thin width (<50 nm). Graphene ribbons were introduced as a theoretical model by Mitsutaka Fujita and coauthors to examine the edge and nanoscale size effect in graphene. Now, a team of researchers reports the generation of net spins on chiral GNRs (chGNRs) by ketone functionalization. 1
GNRs are very interesting structures, partly due to their attractive electronic properties. Those properties vary dramatically with changes in the nanoribbon’s atomic structure in terms of width, crystallographic symmetry, dopant heteroatoms, and edge termination. Interestingly, the electronic properties can be modulated even further by the appropriate design of GNR heterostructures. Moreover, magnetic carbon nanostructures exhibit attractive properties that differentiate them from the conventional magnetic systems relying on d or f states, like a weaker spin−orbit coupling and a larger spin delocalization. This enormous tunability of properties is extremely promising for next-generation nanoelectronic, optoelectronic and quantum devices.
However, the high susceptibility of those properties to minimum changes in the GNR structure also indicates the stringent need for atomic precision in GNR synthesis. In particular, the synthesis and characterization of graphene π-magnetism has seen great advances thanks to the recent development of on-surface synthesis. The topologies of GNRs can be precisely tuned by the rational design of precursor molecules. Because of their delocalized π-magnetism, magnetic GNRs are ideal candidates for the construction of interacting electron spin systems.
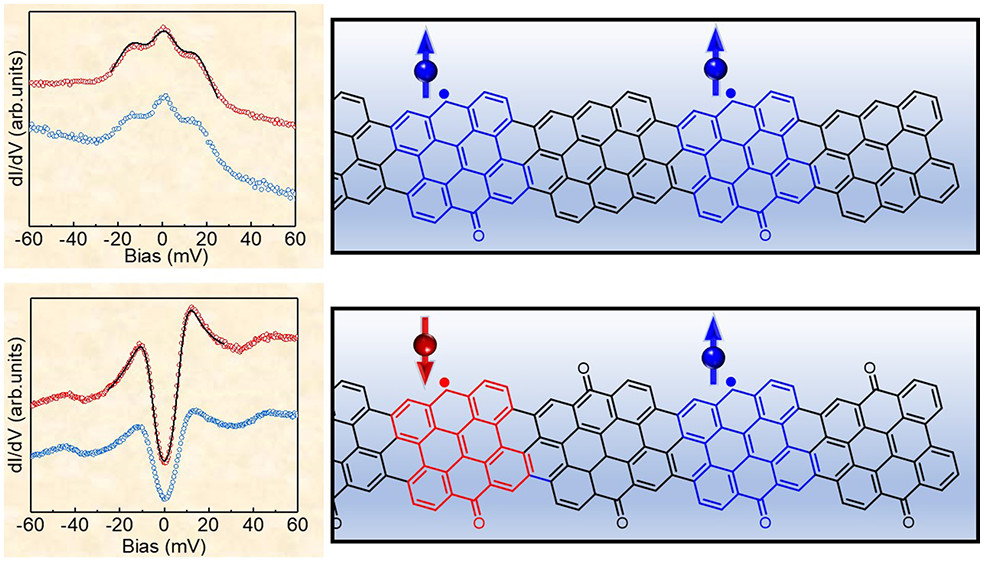
When talking about molecules, “open shell” signifies that there are unpaired electrons. In terms of molecular orbital theory, it means that some molecular orbitals are singly occupied. Organic open-shell compounds are extraordinarily attractive materials for their use in molecular spintronics. The researchers replaced a CH at the pristine chGNR edge by a C=O (carbonyl), adding one π-electron to the system. As a result, the odd number of total electrons causes the appearance of a π-radical.
A similar scenario occurs for regular ketone-functionalized chGNRs in which one ketone is missing, i.e., if a C=O is replaced by a CH. The introduction of a second radical may either maintain the system’s open-shell character or result in their hybridization into a closed-shell structure. Based on this fact, a variety of radical pairs with different geometries were analyzed in several experiments.
The team combined scanning tunneling microscopy (STM) with theoretical calculations, mainly DFT, but also mean-field Hubbard (MFH), given its greater simplicity and successful application to many open-shell carbon nanostructures. This approach revealed how the exchange coupling between two radicals shows remarkably large variations depending on their relative location on the same or opposite sides of the GNRs, on the spatial distance between them, on the chiral asymmetry, as well as on the structure of the GNR surrounding the magnetic state.
These results provide valuable information on the potential use in the design of graphene-based spin chains and networks with tunable magnetic structures. Additionally, the MFH approximation was shown to model systems including oxygen heteroatoms through a minimal extension, which may greatly expedite the understanding and engineering of GNR-based structures in the future.
Author: César Tomé López is a science writer and the editor of Mapping Ignorance
Disclaimer: Parts of this article may have been copied verbatim or almost verbatim from the referenced research paper/s.
References
- Tao Wang, Sofia Sanz, Jesús Castro-Esteban, James Lawrence, Alejandro Berdonces-Layunta, Mohammed S. G. Mohammed, Manuel Vilas-Varela, Martina Corso, Diego Peña, Thomas Frederiksen, and Dimas G. de Oteyza (2022) Magnetic Interactions Between Radical Pairs in Chiral Graphene Nanoribbons Nano Letters doi: 10.1021/acs.nanolett.1c03578 ↩