Euclid’s fifth postulate, the inside story
I am these days reading the delightful (though at times quite demanding) Reviel Netz’s A New History of Greek Mathematics, and I have not resisted the temptation of sharing with you some of the many pearls it contains. One of the most interesting aspects of the book is that it is not a mere ‘survey’ of what we know about ancient Greek mathematics, but constantly tries to offer a kind of ‘socio-cultural’ explanation of the (often) very feeble data we have; that is, it makes the effort of help us to imagine how what we don’t know might have been, so that our data are what they are. It’s very illuminating, for example, his explanation of the origin of the mathematical treatise as a literary genre, around the last decades of the 5th century BC, what contrasted with any mathematical practices before that date, that were intrinsically linked to oral transmission, and gave no place for something like authorship: in fact, all attributions of some ‘theorems’ to people prior to that time, like Thales or Pythagoras, is many centuries posterior and totally legendary. This happened exactly at the same time of authorship/publication started for many other genres.
In a similar way, I find fascinating Netz’s description of the dynamics of the rise and decline of the ‘generations’ of mathematicians, looking for the historical (institutional, political) factors that may have made some ‘generation’ being much more prominent than others: for example, the first ‘great’ generation (that between Archytas and Eudoxus, with Theaetetus as the central figure) being mainly inspired by the awe their discoveries produced on philosophers (like Plato), whereas the second big one (that of Archimedes, Apollonius or Eratosthenes, more than one century later) being devoted to ‘pure technical’ advances rather than to questions that may have some ‘philosophical appeal’, and this in part because of the institutionalisation of the philosophical schools in Athens, that became concentrated on ‘internal’ metaphysical and ethical discussions for which ‘purely scientific’ problems were of little interest. This would explain, for example, why Archimedes’ generation would have basically ignored problems in musical theory (so important one century before and a few centuries later, with the blooming of Neoplatonism), for they were seen as too ‘philosophical’.

But the main point I want to write today about corresponds to something that happens exactly between these two great generations (so, around the end of the 4th century BC), a period in which, curiously, many fewer authors seemed to have been working on mathematics as compared to just the generations preceding and following, but that, however, produced what for us (and for subsequent mathematicians, as testified by the numbers of copies made of it) was nothing else than the most important mathematical work of the ancient world: Euclid’s Elements. As for the content of book itself, the consensus among historians is that little of it are original discoveries by Euclid, for it is basically a compendium of what had been discovered by the previous generations. Perhaps the 20th proposition of book IX (the theorem according to which there is no limit to the quantity of prime numbers, what is actually known as ‘Euclid’s theorem’) is actually by Euclid himself, for we don’t have hints about previous mathematicians that may have been working in the close vicinity of that type of problems, but out lack of evidence is so big that perhaps even this amazing result was the work of some (now) totally forgotten author. I will not, however, go into a general explication of the Elements, but concentrate on a very small, but very important, question, that relates nevertheless to what is most ‘philosophically’ famous about the book: the fifth and last of its ‘Postulates’, which actually reads as follows:
If a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.
(Note that, while this is traditionally known as ‘the parallels postulate’, it explicitly talks about non parallel lines: the two straight lines with which the first one crosses, actually meet at some point, so the postulate claims). This postulate created headaches for centuries, mainly because it looks so different to the other four postulates, the longest of which (in the translation I am using) contains only 11 words (it says, even more shortly, that any straight segment can be prolonged), whereas the fifth postulate contains four times that. So, later mathematicians (with the first exception of the Persian Omar Khayyam, around 1100 CE) didn’t put into question the truth of Euclid’s last postulate but doubted much that it had to be a postulate, instead of a theorem derivable from the other postulates and simpler theorems (after all, there are theorems in the Elements that sound much simpler and more intuitive than it). Actually, the fifth postulate is not used by Euclides till he tackles the proof of proposition 34 in Book I (the theorem stating that the diagonal of a parallelogram divides it in two equal triangles), when he starts the intricate way leading to his proof of the Pythagorean theorem (proposition 47), which is the culmination of Book I, and the real raison d’être of the postulate. But this is shocking because Euclid’s proof (what Renaissance mathematicians called ‘the Windmill’) seems unnecessarily complex and non-intuitive, however beautiful it is.
In fact, it now seems clear that Mesopotamians must have known the theorem probably a full millennium before Euclid. Ancient Greeks referred to it as ‘the schoolchildren result’, and only started attributing it to Pythagoras by the first century BC (that is, around five hundred years after his death). So, very probably the theorem is simply part of the numerous elementary properties of triangles, squares, and rectangles the Greek inherited from Babilonians. The simplest ‘proof’ comes rather straightforwardly on reflecting about a rectangular triangle divided by a height which connects its right angle with the hypotenuse (i.e., points C and H in figure 1): the three triangles, ACB, AHC and CHB (the middle point is chosen to coincide with the right angle) are similar to each other, and a little bit of mental tinkering (something Mesopotamian scribes had plenty of time to spend in) leads easily to realize that AH is to AC as AC is to AB (hence AC2 equals AH times AB), and that HB is to CB as CB is to AB (hence CB2 equals HB times AB). So, AC2 plus CB2 equals AHxAB plus HBxAB. But AHxAB + HBxAB is (AH+HB)xAB… and since AH+HB is AB (i.e., the hypotenuse of the biggest triangle), we have that AC2 + CB2 = AB2. Voilà!
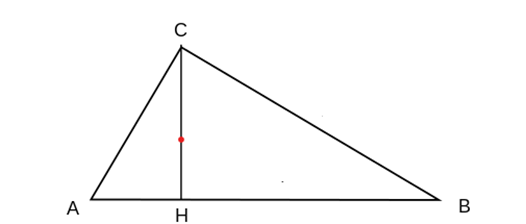
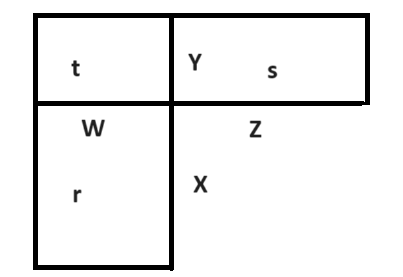
The question is, why such an elementary proof, which was little more than children play for ancient Greeks, was not employed by Euclid in the Elements, where, instead, we have not only a much more convoluted demonstration, but one that requires nothing else that the introduction of the ‘grotesque’ parallels postulate? The answer, Netz reminds us, lies in the apparently innocent step from “AH is to AC as AC is to AB” to “AC2 = AHxAB” (and the similar step about cathetus CB). This looks ‘innocent’ for us, because we tend to interpret the first expression like an equality between fractions: “AH/AC = AC/AB”, but this was not so for Greeks (nor surely for Mesopotamians). They thought about this kind of relations as relations between proportions, and these proportions could be not only between numbers (which for they mean what for us are ‘natural numbers’), but between geometrical figures in general (or between anything, from sounds to ontological domains; a proportion is after all nothing but an analogy, and you can find analogies between no matter what). It is not that Greeks before Euclid (or Babilonians, by the way) could not see that if line X is to line Y as line Z is to line W, then the rectangle XW (r, in the second figure) has the same area as the rectangle YZ (that is, s), which is all that is needed by proving the Pythagorean theorem. (The proof is simply that rectangle r is to rectangle t as segment X is to segment Y, and rectangle s is to rectangle t as segment Z is to segment W, and, since X is to Y as Z is to W, this entails that r and s must be equal to each other).
Euclid himself provides a proof of this (or not exactly: in his inimitable superior elegance, he provides a general proof for parallelograms, not merely for rectangles). But this is proposition 14 of book VI, five books and one hundred theorems after he proved Pythagoras’. Why couldn’t he have gone into this apparently simple stuff before, and give a proof of Pythagoras’ much easier and very likely closer to the historical facts? The reason, Netz reminds us, is nothing else that Euclid’s obsession with proving everything from the most elementary assumptions, where ‘elementary’ does not only mean ‘simple’, but also (we’d say) uncontentious. But, we might retort, “dear Euclid, what the hell can be ‘contentious’ with something as crystal-clear as the three rectangles of figure 2?”
Euclid would have answered us with a smile: “What is what you mean by ‘equality of proportions’? The meaning of that is what has to be as crystal-clear as possible. When you say that ‘X is to Y as Z is to W’, what do you mean exactly?”. And that, before the adoption of real numbers, almost two millennia later, is devilishly difficult to explicate (well, if our notion demanded the introduction of reals, it is because it is not so ‘simple’ after all). Euclid, of course, does explicate the meaning of that, at the beginning of book V, which is the introduction to the theory of proportions. This surely he took it from who probably was the giant amongst the first generation of mathematical giants, Eudoxus. The definition is, however, astonishingly complex (as compared to other definitions, like in the case of the fifth postulate):
Magnitudes are said to be in the same ratio, the first to the second and the third to the fourth, when, if any equimultiples whatever are taken of the first and third, and any equimultiples whatever of the second and fourth, the former equimultiples alike exceed, are alike equal to, or alike fall short of, the latter equimultiples respectively taken in corresponding order.
Don’t be ashamed if you haven’t understood much of this. In more modern parlance it would be equivalent to saying that A is to B as C is to D, if and only if for any natural numbers m and n, it happens that:
mA > nB if and only if mC > nD
mA < nB if and only if mC < nD
mA = nB if and only if mC = nD
Hence, the proportionality between whatever possible ratios (that can be commensurable… or incommensurable, like the proportion between 2 and its square root), I mean, the very notion of ‘proportionality’, could only be understood by Greek mathematicians as a relation between the four terms in the proportion (A, B, C and D)… and all the infinite possible couples of (natural) numbers! You need to take into account the infinity of numbers in order to just make sense of the (apparently innocent and simple) idea of ‘proportion’! We can imagine, hence, poor Euclid walking along Alexandria’s seafront while he was planning the general design of his magnus opus, and stopping at a dilemma that surely kept him sleepless for months, if not for years: “Do I prove the ‘schoolchildren result’ by means of the theory of proportions, as everyone does, what will make it depend on that utterly bizarre definition of ‘being in the same ratio’? Or do I do it by means of this apparently more innocent postulate about straight lines that end crossing at some finite distance if they are not parallel to each other?”. Finally, Euclid slept again by opting for the latter, but that created insomnia to his heirs for more than two millenia, as we perfectly know.
Reference
Netz, R., 2022, A New History of Greek Mathematics, Cambridge University Press.