A brand-new playground for twistronics based on M points

When you look at a crystal—say, a piece of salt or a sheet of graphene—its atoms are not randomly scattered. They form an orderly grid, like tiles on a floor. Because the atoms are arranged in this repeating way, electrons moving through the crystal don’t behave as if they’re in free space. Instead, their motion reflects the crystal’s periodic structure.

Physicists often describe this motion in momentum space (also called reciprocal space) rather than in real space. In real space, you think about positions: where the atoms are, where the electrons go. In momentum space, you think about the waves associated with electrons—their wavelengths and directions. Since electrons in a crystal act like waves, momentum space is the natural stage to describe how they propagate and interfere.

M points

The basic repeating unit of momentum space is called the Brillouin zone, which you can imagine as a kind of “map” of all the distinct electron wave behaviours allowed by the crystal’s periodicity. On this map, certain points stand out:

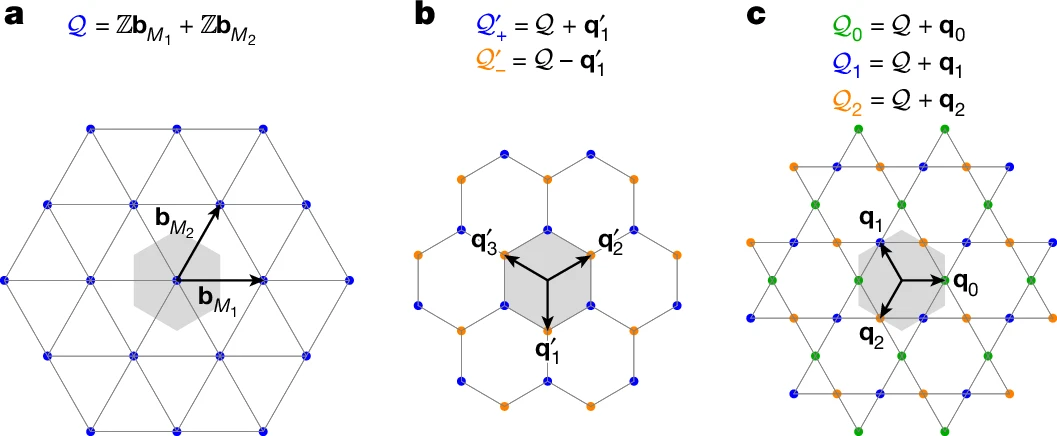
The Γ point, right at the centre, describes electrons with very long wavelengths.

The K points, sitting at the corners, often control exotic behaviours in graphene-like systems.

The M points, lying at the midpoints of the edges of the Brillouin zone, have usually been less explored.

A new research focused ¹ precisely on these M points and unearthed a brand-new toolkit for materials designers.

The energy landscape of a moiré pattern

If you take two atom-thin sheets of certain materials and gently rotate one relative to the other, a delicate interference pattern—called a moiré pattern—appears. This doesn’t just look pretty; it reshapes the Brillouin zone of the stacked system. Suddenly, electrons find themselves in a new energy landscape defined by the moiré periodicity.

The magic happens when this reshaping produces flat bands. Normally, the energy of an electron changes a lot depending on its momentum—it “disperses.” But in a flat band, the energy barely changes as momentum changes. That means the electrons are not zipping around much; their kinetic energy is suppressed. When electrons can’t run freely, their interactions with each other—repulsion, attraction, collective organization—dominate. This is the recipe for fascinating collective behaviours like magnetism, superconductivity, and more exotic correlated phases.

Most moiré systems studied so far—like twisted bilayer graphene—achieve flat bands by focusing on the Γ or K points of their Brillouin zones. What this new study does is shift attention to the M points. At these locations, the electronic states come in threes, like three equivalent “valleys” arranged by symmetry. Twisting two sheets of materials such as SnSe₂ or ZrS₂ lines up these valleys in a way that produces extremely flat bands.

Almost one-dimensionality

The researchers also found that the interference patterns in momentum space resemble a kagome lattice—a web of triangles and hexagons familiar from basket-weaving. Even though the atoms themselves aren’t arranged this way, the effective wave patterns of electrons in momentum space follow this geometry, which is known to host rich quantum phenomena.

An especially intriguing feature is that, depending on the exact stacking of the layers, the electrons may act as if they are confined along one direction—almost like a one-dimensional system—even though the material is two-dimensional. This “quasi-1D” behaviour could lead to entirely new kinds of electronic phases.

New playground for twistronics

The practical upshot is that the M-point strategy offers a brand-new playground for twistronics, the field that studies how twisting layers controls electron behaviour. Instead of relying only on Γ- or K-point physics, researchers now have a whole new toolkit—three valleys, flat bands, kagome-like structures, and tuneable dimensionality—to explore and potentially engineer states of matter that don’t occur naturally.

In summary, this work shows that by twisting atom-thin crystals in just the right way, we can design quantum materials whose electrons live in a strange new landscape—one where their motion is slowed, their interactions amplified, and their collective behaviours open a window to physics we’ve only begun to imagine.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance

Disclaimer: Parts of this article may have been copied verbatim or almost verbatim from the referenced research paper/s.