How charge and spin interact in any diffusive system with SOC

Imagine electrons as tiny particles zipping through a material, each carrying two key properties: charge, which powers our everyday electronics, and spin, like a little internal compass needle that points up or down. Charge flow is what we call electric current, but spin adds a magnetic twist, opening doors to advanced technologies like more efficient computers or sensors. The catch? In most materials, charge and spin don’t interact much. But in some, a phenomenon called spin-orbit coupling (SOC) links them. SOC is a relativistic effect—think Einstein’s ideas at play on a tiny scale—where an electron’s motion creates a magnetic field that tugs on its spin, much like how Earth’s orbit around the Sun couples to its spin on its axis.

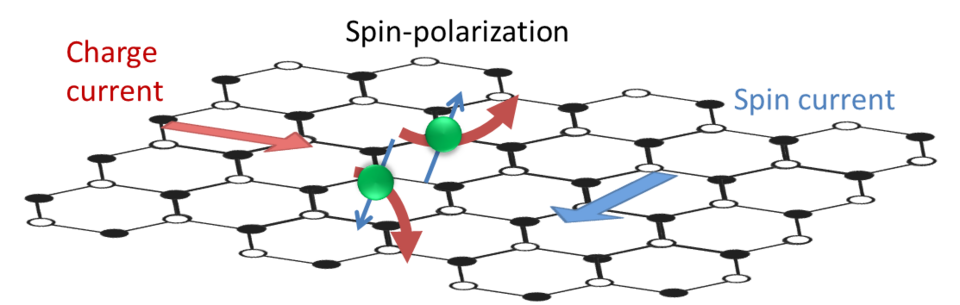
This coupling enables “spin-charge interconversion,” where electric currents can generate spin accumulations, and vice versa. It’s the foundation of spintronics, a field aiming to use spin for faster, lower-power devices. Two classic examples are the spin Hall effect, where a charge current deflects electrons with opposite spins to different sides of a wire, creating a “spin current” perpendicular to the charge flow, and the Edelstein effect (also known as the spin-galvanic effect), where a current induces a net spin polarization in materials lacking mirror symmetry.

Real-world experiments often involve messy, disordered samples—think impurities or defects scattering electrons like bumps on a road. At low temperatures, superconductivity can kick in, where electrons pair up and flow without resistance. Traditional theories struggle here because they rely on simplified models that don’t capture complex SOC in real crystals or the full range of temperatures and conditions.

A testament to symmetry’s power

Now, a groundbreaking paper ¹ introduces a universal framework for describing how charge and spin interact in diffusive (disordered) metals and superconductors with any SOC allowed by the material’s crystal symmetry. Instead of starting from a specific microscopic model and grinding through calculations, they build an effective theory based purely on symmetries—fundamental rules that the system must obey, like charge conservation or the crystal’s geometric structure.

This approach mirrors the Ginzburg-Landau theory, a phenomenological model from the 1950s that describes superconductivity near the critical temperature by expanding the free energy in terms of an “order parameter” (a measure of how superconducting the material is). But the new theory goes further: it’s valid at all temperatures, handles nonequilibrium situations (like driven currents), and covers normal metals too. It even includes superconducting fluctuations, those brief hints of pairing above the transition temperature.

From a Keldysh nonlinear sigma model…

At the heart is the Keldysh nonlinear sigma model (NLSM), a mathematical tool from quantum field theory adapted for condensed matter. The NLSM describes the system’s behavior through a matrix field that encodes the quasiclassical Green’s functions—essentially, probabilities for electron propagation. By imposing symmetries like charge conjugation (a way to relate particles and holes) and time-ordering (ensuring cause precedes effect), the authors fix the form of the NLSM action, the “energy functional” of the theory. Crystal symmetry then dictates which terms are allowed, like those for anisotropic diffusion or spin relaxation.

…to a generalized Usadel equation

From this, they derive a generalized Usadel equation, the workhorse for diffusive superconductors. This equation captures all symmetry-permitted effects: spin relaxation (spins losing alignment over time), precession (spins rotating like tops), spin Hall, spin current swapping (exchanging spin and flow directions), and spin-galvanic couplings.

The universal spin-galvanic relation

One standout result is the universal spin-galvanic relation. A tensor called γ connects excess spin to charge current: current = γ · spin. This holds everywhere—normal metals, superconductors, equilibrium or not. It’s “universal” because symmetry enforces it, regardless of microscopic details; experiments just measure γ for a given material.

In superconductors, this leads to fascinating predictions. Supercurrents act like effective magnetic fields, inducing spin textures around vortices—swirling regions where the superconducting order winds like a whirlpool. The theory shows how these textures depend on crystal symmetry, explaining effects like the superconducting diode (current flows easier one way) or phase shifts in Josephson junctions (tunnels between superconductors). For instance, in gyrotropic crystals (those with handedness, like a spiral staircase), spins around a vortex point in patterns determined by γ, as shown in the paper’s calculations.

Random walkers in a crowded room

Physically, picture electrons diffusing like random walkers in a crowded room. SOC adds a twist: each step slightly rotates the spin based on direction and crystal environment. Over many steps, this builds up effects like spin deflection (Hall) or net polarization (Edelstein). The theory collects these into a compact action, from which equations flow naturally.

For researchers, it’s a “lookup table”: Know your crystal’s point group (symmetry class), and the allowed couplings pop out. Measure a few coefficients like γ, and predict currents, spins, or vortex behaviors without custom models. It extends to broken time-reversal (with magnets) or interfaces with strong SOC, like in heterostructures.

This work unifies scattered phenomena into a clean, testable framework, bridging high-energy physics tools with real materials. It’s a testament to symmetry’s power: from messy electrons emerges elegant order. As spintronics pushes toward practical devices, such universal theories will guide the way, turning quantum quirks into technological triumphs.

Author: César Tomé López is a science writer and the editor of Mapping Ignorance

Disclaimer: Parts of this article may have been copied verbatim or almost verbatim from the referenced research paper/s.