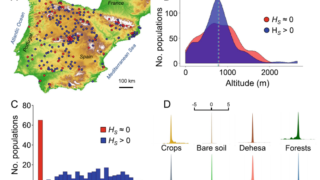
Synchrony with chaos
Imagine an old-growth forest in the fading light of a summer evening. As the last of the sun’s rays disappear beneath the horizon, a tiny flash catches your eye. You turn around, hold your breath; it blinks again, hovering 2 feet above the leaf litter. Across the dusky glade, a fleeting response. Then another one […]