Finding a shortest route is not easy for a watchman patrolling streets

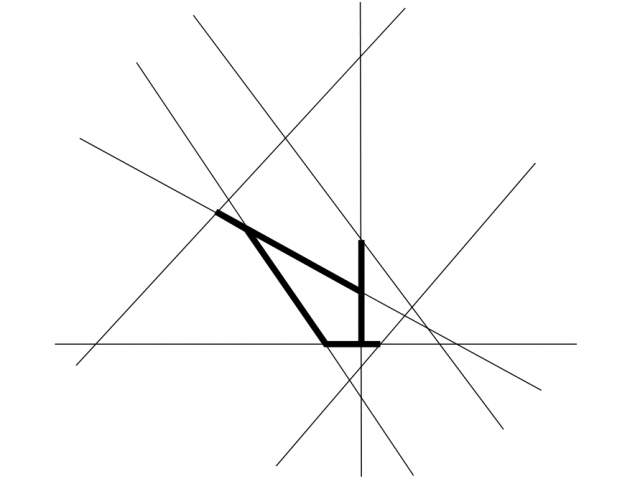
Imagine you were a watchman, having to patrol some streets. Today you were assigned to straight, well-illuminated, and wide streets, that can be checked with a glance from the intersection.

Before starting the route, you want to determine the shortest route allowing to check all your streets. How difficult can this be?

Dumitrescu et al.¹ study the complexity of this watchman route problem, for which a more formal statement needs a couple of easy definitions: First, a set of lines is said to be connected if, for any pair of points on them, it is possible to travel between the two points moving along the given lines. This turns out to be equivalent to not all the lines being parallel (which is most likely the case for streets).

Second, a watchman route in a set of lines is a closed polygonal path along them, such that every point on the given lines is visible from at least one point of the path. Note that the path has to be closed, i.e., the initial and the final points must be the same (so that the watchman goes back to the headquarters).

Now one can formally state:

The Watchman Route problem for Lines (WRL):

Given a connected set of lines, find a shortest watchman route.

Analogously, replacing lines by segments in the two definitions above, one can also consider:

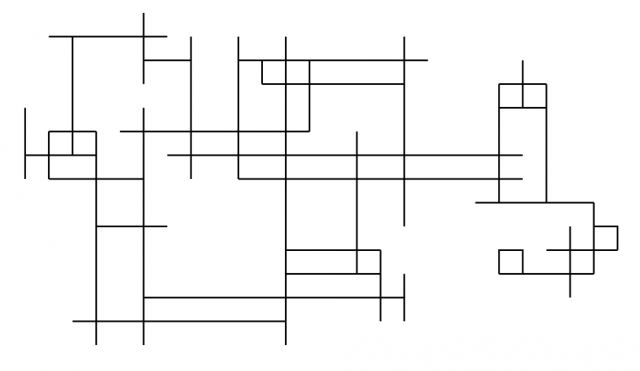
The Watchman Route problem for Segments (WRS):

Given a connected set of segments, find a shortest watchman route.

Although these problems remind to the well-known Traveling Salesman Problem, Dumitrescu et al. prove that the Watchman Route problem for Lines (WRL) in 2D can actually be solved in polynomial time , also for the variant in which only a subset of the given lines needs to be visited and you are allowed to move along the whole set of given lines. Their proof is via solving a related Minimum Convex Hull problem, for which dynamic programming is used.

On the contrary, the authors prove that the Watchman Route problem for Segments (WRS) in 2D is NP-hard, even for axis-aligned segments. Their proof adapts that from Dumitrescu and Tóth ² for the NP-hardness of computing a shortest watchman route in a polygon with holes.

Furthermore, Dumitrescu et al. prove that the 3D version of the Watchman Route problem is also NP-hard, both for lines (WRL) and segments (WRS), even in the case of orthogonal lines or segments. Indeed, their proof relates these problems to the Geometric Traveling Salesman Problem ³⁴, which is known to be NP-hard for both the orthogonal and the euclidean metrics ⁵.

Finally, Dumitrescu et al. show that the randomized approximation algorithm by Fakcharoenphol et al. ⁶ yields an approximation ratio for the Watchman Route problem for segments (WRS) in any dimension. For the 2D case, a deterministic algorithm with a better approximation ratio has been later proposed by Mitchell ⁷.

In addition, the authors consider some special cases of the Watchman Route problem for Segments (WRS), for which they are able to provide an improved approximation or an exact algorithm. The first one is the case in which the segments do not intersect too much, meaning that there are at most intersection points on each segment. Then, there is a polynomial-time algorithm for the WRS with an approximation factor of .

The second special case is that of outerplanar grids, an arrangement of axis-aligned segments such that every segment has a point on the (boundary of) the outer face of the arrangement. In this case, they show that the WRS can be solved in time.

As a coda, let me bring here two of the interesting open problems suggested in the paper:

• Can the 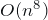running time of the algorithm for the Watchman Route problem for Lines (WRL) in 2D be improved?

• What is the complexity of the watchman route problem for planes in 3D?