Quantum Thermodynamics III: Quantum thermal machines

One of the most important features of thermodynamics is that it has improved human quality of life amazingly during the last centuries. Since in 1606, the Spanish inventor Jerónimo de Ayanz y Beaumont patented the first steam engine a great effort has been done in developing new and better thermal machines. Internal combustion engines, heat pumps and refrigerators are some of the principal heat machines used nowadays.

Certainly, the main theoretical milestone for the developing of thermal machines was performed by the French military engineer Sadi Carnot, by deriving the cycle of maximum efficiency. This reversible cycle is also known as the Carnot’s Cycle ¹and the ideal machine that performs it is called Carnot’s Engine. This ideal engine works between two thermal baths with different temperatures (T_C for the cold bath, and T_H for the hot one), and its efficiency is given by a simple relation . This efficiency is the maximum allowed by classical thermodynamics, and all thermal machines are limited by it.

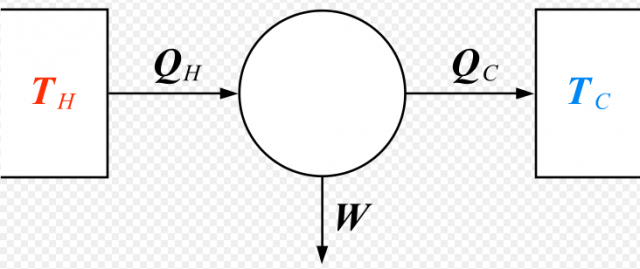
As we have explained before in other posts of this series, thermodynamics is a macroscopic theory, and its applications to microscopic systems is still not clear. Only recently, the possibility of creating a microscopic refrigerator, based on quantum mechanics’ rules, has been developed. In Refs ²³ physicist from United Kingdom discuss the problem of finding the set of smallest heat machines, and the thermodynamic properties of such set. In these works it is probed that a very simple model of heat machine can be performed just by the use of three two levels systems, or qubits (for quantum bits). In their first paper [2], they design a refrigerator by this technique. In this model each of the qubits is connected to a thermal bath and also between them. One of the baths represent the object to be cooled, the second one represents a hotter environment to where the heat should be delivered. Finally, the third bath has the role of providing energy for the cooling, as is shown in Figure 2(a).

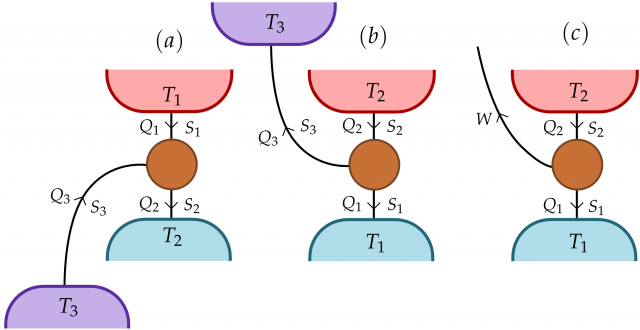
The same group extended the idea of this refrigerator [3] to other thermal machines as heat pumps. One main result of this analysis is that the microscopic heat machines, and only them, can approach the maximum efficiency of Carnot’s cycle. Also, the efficiency of such machines is universal, depending only in the temperatures of the baths and not in details as the coupling between the qubits and the baths. This result is very different of what we find in macroscopic thermal machines, where the efficiency depends on many parameters and it is always below Carnot’s efficiency. Skrzypczyk et al argue that this different behavior from microscopic to macroscopic machines is due to the fact that many microscopic machines compose a macroscopic one. It is the way of composing them what breaks the universality of the efficiency and what reduces it from the maximum one.

Another interesting question to address is if quantum systems allow doing tasks that are forbidden classically. It is well know that quantum systems can perform certain tasks, like computing, in a way forbidden for classical systems. Maybe, they can also perform different thermal processes. That is the idea analyzed in Ref ⁴ where a procedure for extracting heat from a single bath via quantum coherence is proposed.

Before discussing the results of Ref. [4] let see what classical thermodynamics has to say about this problem. Just by analyzing the maximum efficiency formula, , we can conclude that when the temperature of the hot and cold baths are equal the efficiency is zero. Because of that, it is impossible to create any kind of thermal machines that operates under these conditions. A hypothetical machine that performs this operation also violates the Second Law of Thermodynamics (see previous post) and it can be considered as a “perpetual mobile of second kind”. On the other hand, that applies only for machines that work in a steady state, meaning that the machine should be able to extract heat in a continuous way. There is no rule that forbids to have stored a certain potential energy, as a mass at a certain height, and use it to extract a finite amount of heat from a single bath. What is done in [4] follows this idea, but instead of potential energy they use a quantum property, called “phaesonium”. As this phaesonium can be used only one, a cycle cannot be performed without an external energy source and the second law is preserved.

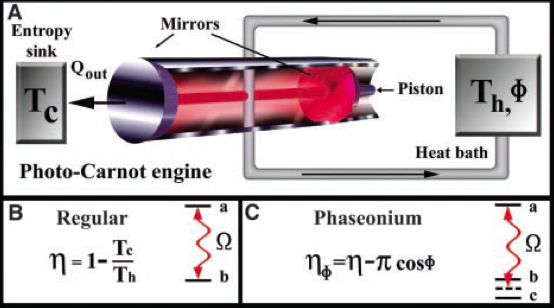
The concrete machine proposed is called a photo-Carnot engine. It is based in a piston full of three level atoms (or qutrits) in a microwave cavity. The technical details of this engine are beyond the purpose of this post, but we can discuss their physical foundations. By the use of the quantum coherence, meaning the property of being in more than one state, of the atoms a property called detailed balance can be broken. Detailed balance tells us that if a system is in equilibrium the probability of having a fundamental process or its reverse should be equal. Because of that, systems at equilibrium remain at equilibrium, because all processes happen in the same ratio as their reverses. Hence, if by the use of quantum coherence detailed balance can be avoided, the system can be driven out of equilibrium and it can perform a work. Unfortunately, the quantum coherence of the atoms is lost in the process and it should be “refueled” in order to make the engine to work again. Because of that, there is not possibility of creating a perpetual mobile, but the design opens a door to a new kind of thermal quantum machines.

Another interesting and useful kind of thermal machines, where quantum processes play a relevant role are photocells. The work on this direction is huge and interesting for practical purposes and, because of that, the next post of this series will be entirely dedicated to it.