In how many ways can you fold a strip of stamps?

When was the last time you used a postage stamp? Even if it was a long time ago, you may have hold in your hands a strip of stamps. Maybe you have even tried to fold it into a stack, one stamp wide, so that the strip was easier to store. Have you ever wondered how many ways are there to do so?

This problem was stated by Lucas ¹ in 1891 and today, more than 120 years later, there is still no formula answering the question. A recent paper by Stéphane Legendre² reviews the problem and adds some new results.

First, the labeled case is considered, where the stamps can be distinguished (as in the previous picture). For a mathematical model, you can label them consecutively along the unfolded strip. The goal is then to find all the possible stacks being stamp wide and stamps tall.

The following figure shows all the possibilities for a strip of stamps. Horizontal segments represent the stamps, while vertical segments represent the perforations. In addition, the label of each stamp is depicted next to it.

Those strings of numbers suggest to consider a useful notion in Mathematics, that of a permutation. Reading the labels downwards, from the top of the stack to the bottom, we can unambiguously identify a folding with a permutation. Interestingly, not all the possible permutations lead to feasible foldings: For an example, the permutation is not a folding because a crossing would show up.

The question of which permutations do correspond to a folding was settled by Koehler³ in 1968:

A permutation is a folding if, and only if, neither the inequalities

nor any of their circular rearrangement occur with and having both the same parity (odd or even).

Note that in the example above, the inequalities arise for and .

As for the question of the number of foldings, Sainte-Laguë⁴ observed in 1937 that:

The number of elements of the set of foldings of labeled stamps is

,

where is the number of elements of the set of -foldings of type , i.e., with stamp 1 on top.

This allows to focus on the set which, usefully, can be constructed in an inductive way by using a tree of depth . The following figure shows the tree describing the sets for .

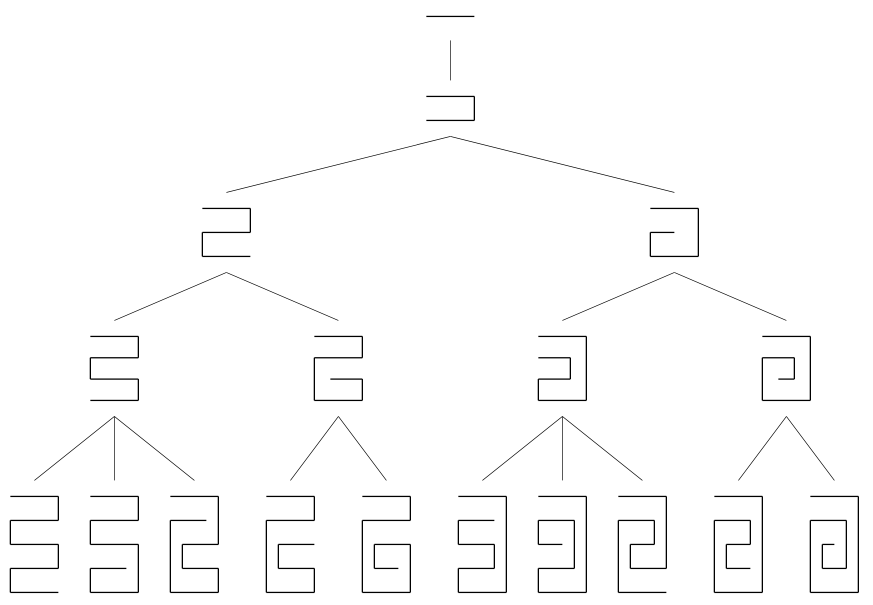
It turns out that, below the second level, the left and the right subtrees are topologically identical. The reason is that if is a folding, then the “reversed” permutation is also a folding.

Thus, each folding in the left subtree is uniquely associated with a folding in the right subtree. This implies that is even for and, more important, that the problem can be reduced to focusing on foldings of type . Lunnon⁵ proposed an algorithm for listing these foldings, using a depth-first search.

The above results have allowed to compute the number of labeled foldings up to , for which 37384929247793935264200 possibilities arise. The whole list of numbers can be checked as the sequence A000136 of the On-Line Encyclopedia of Integer Sequences⁶.

The case of blank stamps is also considered by Legendre. In this case the stamps are not labeled, so that the foldings have to be distinguished according to their shapes. In particular, different labeled foldings might lead to the same unlabeled folding. For an example, consider the second and fourth cases (left to right) in the first row of Figure 2, being one a reflection of the other.

Luckily enough, the corresponding set of unlabeled foldings can also be constructed inductively using a tree. The following figure shows the foldings of blank stamps for .

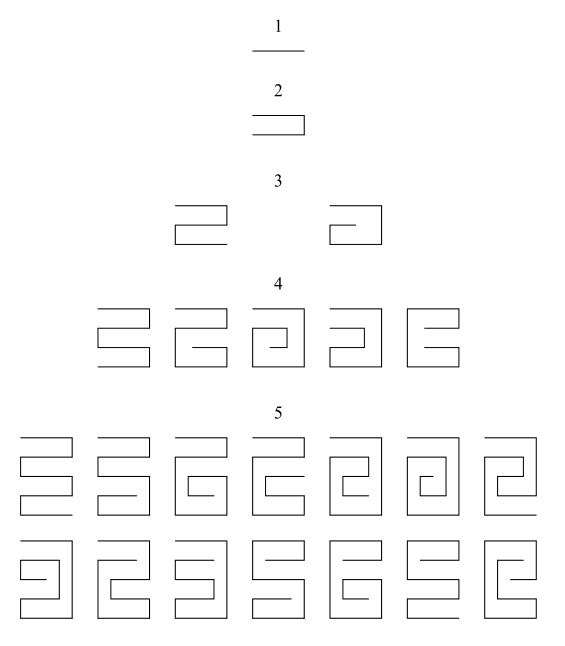
Again, the number of different unlabeled foldings is known up to , for which 9346232311986692725748 possibilities arise. The whole list of numbers is available as the sequence A001011 of the On-Line Encyclopedia of Integer Sequences⁷.

Provided that there is no formula for the number of foldings, a classical question is wondering about the asymptotics. I.e., how is this number growing when grows? Legendre cites several authors to support the general believing that the number of -foldings is of the form , with being constants which, of course, are not known. That is, an exponential growth.

In order to provide an estimation of , Legendre shows that the number of foldings for all the cases considered above, , share the same . Then, he uses the best known values to obtain an estimation up to the tenth decimal position.

Overall, this is a nice review of a problem which, despite seeming harmless, explodes for not so large cases due to the exponential growth of the number of combinations.