A local theory of insulators
We all know what an insulator is, don’t we? An insulator is any substance that is a poor conductor of heat and electricity. Both properties ussually occur as a consequence of a lack of mobile electrons.If we want to dive a little deeper into the nature of insulators we make use of energy band theory, as we saw here, and that’s it. Or not?
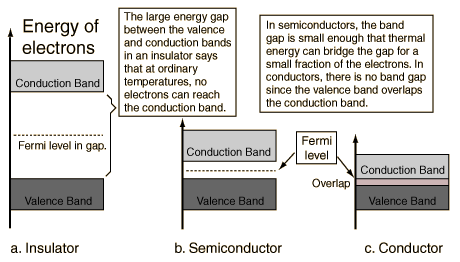
The Fermi level is the energy in a solid at which the average number of particles per quantum state is ½ or, in other words, one half of the quantum states are occupied. The difference between an insulating material and a conducting one is commonly attributed to the spectral properties of the system or to the localization properties of the electronic states at the Fermi level. Thus, The Fermi level in conductors lies in the conduction band, and in insulators and semiconductors it falls in the gap between the conduction band and the valence band. This is the standard explanation.
But a paradigm change occurred in 1964, when W. Kohn defined the insulating state making neither reference to electronic excitations nor to Fermi-level properties: the qualitative difference between insulators and conductors manifests itself also in a different organization of the electrons in their many-body ground state. Recent research has established Kohn’s pioneering viewpoint on a sound formal and computational basis, rooted in geometrical concepts. The theory—as developed so far—addresses only macroscopically homogeneous systems: either crystalline correlated systems or independent-electron systems.
Now, Antimo Marrazzo (EPFL) and Raffaele Resta (IOM-CNR & DIPC) 1 show that that the metallic or insulating character of the electronic ground state can be probed locally.
As we mentioned above, an insulator differs from a metal because of a different organization of the electrons in their ground. This feature has been probed by means of a geometrical property, namely, the quantum metric tensor, which addresses the system as a whole, and is therefore what limits the approach to macroscopically homogenous samples. What the researchers prove is that, using as the sole ingredient the ground state electron distribution, an analogous approach leads to a localization marker, which can detect the metallic versus insulating character of a given sample region, even in the Anderson case (where the spectrum is gapless). It is worth mentioning that the model avoids any reference to either spectral properties or to localization properties of the electronic states at the Fermi level.
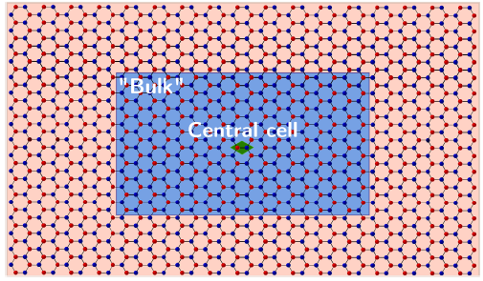
Simulations on several test cases validate the new model. Besides the case of band insulators (model and first principles), test cases include Anderson insulators (where the spectral properties are of no avail) and topological insulators (where the bulk is insulating and the boundary is conducting). When applied to an insulator with a nonzero Chern invariant, the marker is capable of discriminating the insulating nature of the bulk from the conducting nature of the boundary.
The simulations presented by the authors address independent electrons only; still, the researchers argue that this new local theory of the insulating state can be extended to correlated electrons as well. If this proves to be the case, this new marker paves the way for a unified complete theory of the insulating state, including in principle all kinds of insulators, both homogeneous and heterogeneous (crystallites, heterojunctions or nanostructures).
Author: César Tomé López is a science writer and the editor of Mapping Ignorance
References
- Antimo Marrazzo and Raffaele Resta (2019) Local Theory of the Insulating State Physical Review Letters doi: 10.1103/PhysRevLett.122.166602 ↩
1 comment
[…] Material bat isolatzailea den ala ez dioen teoria makroskopikoa izan da orain arte. Beste modu batera ikusita, bere osotasunean kontsideratuta baino ezin du esan teoriak material jakin bat isolatzailea izango den ala ez. Ezin du aurreikusi multzo horren bolumen […]