Mermin–Wagner theorem for practical length scales
Mermin–Wagner
The demand for computational power is increasing exponentially, following the amount of data generated across different devices, applications and cloud platforms. To keep up with this trend, smaller and increasingly energy-efficient devices must be developed, which require the study of compounds not yet explored in data-storage technologies. The discovery of magnetically stable 2D van der Waals materials could allow for the development of spintronic devices with unprecedented power efficiency and computing capabilities that would, in principle, address some of these challenges.
The magnetic stability of van der Waals layers has been one of the central limitations for finding suitable candidates, given that strong thermal fluctuations are able to rule out any magnetism. As it was pointed out by Mermin and Wagner for spins on a lattice, long-range order should be suppressed at finite temperatures in the 2D regime, when only short-range isotropic interactions exist. Importantly, the theorem only excludes long-range magnetic order at finite temperature in the thermodynamic limit, i.e., for infinite system sizes. However, the common understanding is that the theorem also excludes the alignment of spins in samples studied experimentally which are a few micrometres in size, suggesting that such systems are indistinguishable from infinite.
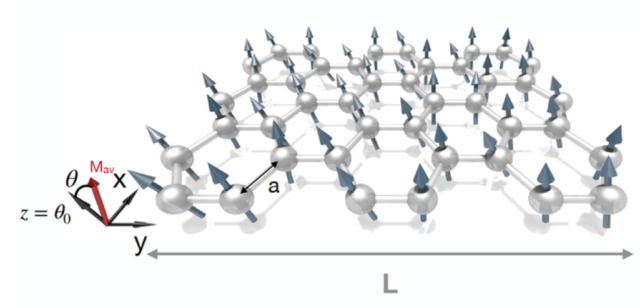
In other words, the Mermin-Wagner theorem states that long-range magnetic order does not exist in one- (1D) or two-dimensional (2D) isotropic magnets with short-ranged interactions. Now, a team of researchers shows 1 that in finite-size 2D van der Waals magnets typically found in lab setups (within millimetres), short-range interactions can be large enough to allow the stabilization of the magnetic order at finite temperatures without any magnetic anisotropy.
An intriguing question on the long-range limit is how we can understand real-life materials, which routinely have a finite size (L), in light of the Mermin-Wagner theorem. As we mentioned above, it is known that thermal fluctuations will affect the emergence of spontaneous magnetization at low dimensionality. Nevertheless, it is unclear which kind of spin ordering can be foreseen in thin van der Waals layered compounds when finite-size effects and exchange interactions play together. But, with recent advances in computational power and parallelization scalability, it is possible to directly model magnetic ordering processes and dynamics of 2D materials on the micrometre length-scale accessible experimentally.
The researchers show that short-range order can exist in systems with no anisotropy, even down to the 1D and 2D limits. By using computer intensive atomistic spin simulations and analytical models, they demonstrate the non-applicability of the Mermin–Wagner theorem for practical length scales and device implementations. They find that the crossover temperature, where the intrinsic magnetization changes from superparamagnetic to a completely disordered paramagnetic regime, is weakly dependent on the system length, requiring giant sizes ( ~ 1026m, of the order of the observable universe, 93 billion light-years) to observe the vanishing of the magnetic order as expected from the Mermin-Wagner theorem.
The large distance character of short-range interactions in 2D van der Waals magnets drives the formation of magnetic ordering at different lattice symmetries, flakes shapes and chemical compositions. The team unveils that exchange interactions are the main driving force behind the stabilization of 2D magnetism and broaden the horizons of possibilities for the exploration of compounds with low anisotropy at an atomically thin level.
More on the subject:
A different class of van der Waals magnets
Proximity effects or the fragility of electronic ground states in 2D materials
The classical nonlinear mechanics of wrinkles in 2D materials
Author: César Tomé López is a science writer and the editor of Mapping Ignorance
Disclaimer: Parts of this article may have been copied verbatim or almost verbatim from the referenced research paper/s.
References
- Jenkins, S., Rózsa, L., Atxitia, U., Novoselov, K.S. & Santos, E.J.G. (2022) Breaking through the Mermin-Wagner limit in 2D van der Waals magnets. Nat Commun doi: 10.1038/s41467-022-34389-0 ↩