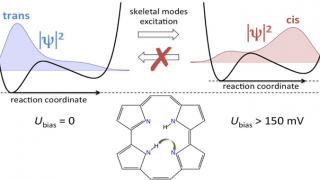
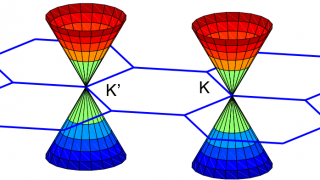
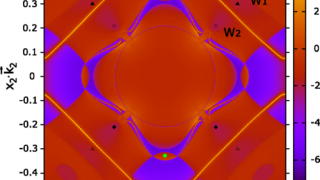
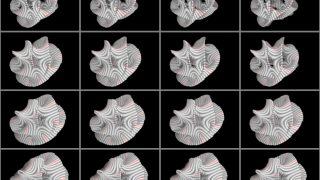
Family unification (2): The SO(18) spinor strikes back
In the previous post, Family unification 1, we reviewed the historical development of Grand Unified Theories (GUT) of force and matter, i.e. Comprehensive Unification. We saw how the SO(18) spinor, 256, is able to accomodate the Standard Model (SM) family structure, however it contains too many families and, also, phenomenologically dangerous mirror families. During the […]