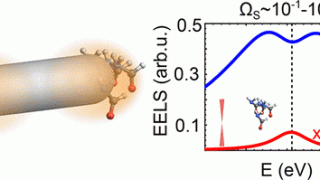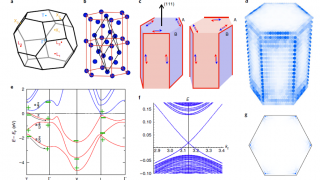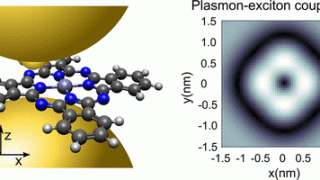
Topology of disconnected elementary band representations
Condensed matter • Materials • Physics • Quantum physics • Theoretical physics
The revolutionary theory of topological quantum chemistry , a description of the universal global properties of all possible band structures and materials, diagnoses topological phases based on elementary band representations. A set of bands is topological if it lacks an “atomic limit” that obeys the crystal symmetry (and time reversal, if desired): formally, an atomic […]