The fascinating history of the brick factory problem
The crossing number of a graph, defined as the minimum number of edge crossings arising when the graph is drawn in the plane, turns out to be a mathematical concept with a fascinating history.
Lowell Beineke and Robin Wilson 1 trace the origins of the crossing number, with particular emphasis in the war-time experiences of the Hungarian number-theoretist Paul Turán (to which this post is devoted) and the geometrical explorations of the British artist Anthony Hill (which are left for a future post).
This is how Paul Turán described the brick factory problem, for the first issue of the Journal of Graph Theory 2:
In July, 1944 the danger of deportation was real in Budapest and a reality outside Budapest. We worked near Budapest, in a brick factory. There were some kilns where the bricks were made and some open storage yards where the bricks were stored. All the kilns were connected by rail with all the storage yards. The bricks were carried on small wheeled trucks to the storage yards. […] The trouble was only at the crossings. The trucks generally jumped the rails there, and the bricks fell out of them; in short, this caused a lot of trouble and loss of time which was rather precious to all of us (for reasons not to be discussed here). […] The idea occurred to me that this loss of time could have been minimized if the number of crossings of the rails had been minimized. But what is the minimum number of crossings? I realized after several days that the actual situation could have been improved, but the exact solution of the general problem with ![]() kilns and
kilns and ![]() storage yards seemed to be very difficult…
storage yards seemed to be very difficult…

This problem might remind you of the houses-and-utilities problem. Of unknown origin, this problem has a number of different formulations 3. All of them show six nodes in the plane, split into two classes of three nodes each, require each node in a class to be connected to all the nodes in the other class, and ask to do it in such a way that no connections cross. It turns out that no solution exists. (A variant of the problem with two classes of four nodes on the torus, proposed in 1961, does have a solution 4).
Using mathematical terms, one can wonder about the minimum number of edge-crossings needed when a graph ![]() is drawn in the plane (it is assumed that only two edges appear at each crossing). This is called the crossing number of the graph
is drawn in the plane (it is assumed that only two edges appear at each crossing). This is called the crossing number of the graph ![]() , denoted by
, denoted by ![]() .
.
The brick factory problem deals with the complete bipartite graph ![]() . When
. When ![]() or
or ![]() is 1 or 2, this graph can be drawn in the plane without any crossing. Here is how to do it for
is 1 or 2, this graph can be drawn in the plane without any crossing. Here is how to do it for ![]() and
and ![]() :
:

However, crossings can not be avoided if both ![]() and
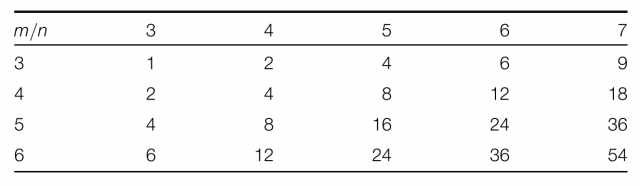
and ![]() are at least 3. The following table shows some values of
are at least 3. The following table shows some values of ![]() :
:
After the war was finished, Turán communicated the brick factory problem to other mathematicians. Almost simultaneously, in 1952 the probabilist Kazimierz Urbanik and the topologist Kazimierz Zarankiewicz proposed solutions to the problem. The solution submitted by Zarankiewicz 5 included the following claim:
Zarankiewicz’s conjecture: The minimum number of crossings in any drawing of the complete bipartite graph
is
.
Zarankiewicz observed that such a number of crossings can be attained by the following construction:
Divide the ![]() vertices into two sets of equal (or nearly equal) sizes and place the two sets equally spaced on the x-axis on either side of the origin. Do the same for the
vertices into two sets of equal (or nearly equal) sizes and place the two sets equally spaced on the x-axis on either side of the origin. Do the same for the ![]() vertices, placing them on the y-axis, and then join appropriate pairs of vertices by straight-line segments.
vertices, placing them on the y-axis, and then join appropriate pairs of vertices by straight-line segments.
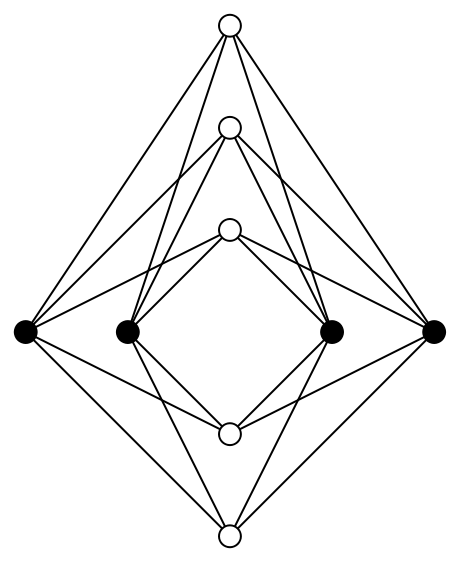
The figure illustrates the construction for ![]() , for which
, for which ![]() crossings arise.
crossings arise.
Unfortunately, Zarankiewicz’s proof was correct for the case ![]() but his inductive argument was wrong. It works when going from odd to even values of
but his inductive argument was wrong. It works when going from odd to even values of ![]() or
or ![]() , but not from even to odd, as the graph-theorists Paul Kainen and Gerhard Ringel observed 6, in an independent way, respectively in 1965 and 1966.
, but not from even to odd, as the graph-theorists Paul Kainen and Gerhard Ringel observed 6, in an independent way, respectively in 1965 and 1966.
Since then, just a few advances on the conjecture have been achieved. In 1970, Daniel Kleitman 7 showed that the conjecture holds when ![]() or
or ![]() is at most 6. In 1993, Douglas Woodall 8 extended the results showing that the conjecture holds for
is at most 6. In 1993, Douglas Woodall 8 extended the results showing that the conjecture holds for ![]() and
and ![]() .
.
Today, more than 60 years later, Zarankiewicz’s conjecture remains open. Is really his scheme the drawing of a complete bipartite graph having the least crossings?
References
- Beineke L. & Wilson R. (2010). The Early History of the Brick Factory Problem, The Mathematical Intelligencer, 32 (2) 41-48. DOI: 10.1007/s00283-009-9120-4 ↩
- Paul Turán. A note of welcome. Journal of Graph Theory. Volume 1, Issue 1 (Spring 1977), pages 7–9. http://dx.doi.org/10.1002/jgt.3190010105. ↩
- David E. Kullman. The utilities problem. Mathematics Magazine. Volume 52, Number 5 (1979), pages 299–302. ↩
- Thomas H. O’Beirne. Christmas puzzles and paradoxes, 51: For boys, men and heroes. New Scientist. Volume 12, Number 266 (21 December 1961), pages 751–753. ↩
- K. Zarankiewicz. On a problem of P. Turan concerning graphs. Fundamenta Mathematicae. Volume 41 (1954), pages 137–145. ↩
- Richard K. Guy. The decline and fall of Zarankiewicz’s theorem. In: Proof Techniques in Graph Theory (ed. F. Harary), New York: Academic Press (1969), pages 63–69. ↩
- Daniel J. Kleitman, The crossing number of
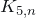 . Journal of Combinatorial Theory. Volume 9 (1970), pages 315–323. http://dx.doi.org/10.1016/S0021-9800(70)80087-4 ↩
. Journal of Combinatorial Theory. Volume 9 (1970), pages 315–323. http://dx.doi.org/10.1016/S0021-9800(70)80087-4 ↩ - Douglas R. Woodall, Cyclic-order graphs and Zarankiewicz’s crossing-number conjecture, Journal of Graph Theory. Volume 17, Issue 6 (December 1993), pages 657–671. http://dx.doi.org/10.1002/jgt.3190170602. ↩
5 comments
The links for references 7 and 8 are broken.
Corrected. Thanks a lot.
[…] previous post presented the fascinating history of the brick factory problem, which wonders about the smallest […]
[…] and Robin Wilson1, which traces the origins of the crossing number of a graph. After focusing on the brick factory problem, proposed by the Hungarian number-theoretist Paul Turán, the second half of the paper is devoted […]
[…] último, puedes encontrar más enlaces e información en la entrada en inglés The fascinating history of the brick factory problem que escribí para Mapping Ignorance y que llegó hasta reddit. En el mismo blog, en la […]