The history of the crossing number of the complete graph
We have already introduced the first half of a paper by Lowell Beineke and Robin Wilson1, which traces the origins of the crossing number of a graph. After focusing on the brick factory problem, proposed by the Hungarian number-theoretist Paul Turán, the second half of the paper is devoted to the crossing number of the complete graph and the geometrical explorations of the British artist Anthony Hill.
Lacking of any formal training in higher mathematics, Anthony Hill described himself as a constructivist working as a geometric formalist and made his way to deserve an Honorary Research Fellow in the Department of Mathematics at University College, London.
Unaware of the brick factory problem (which wonders about the smallest possible number of rail crossings when connecting ![]() kilns and
kilns and ![]() storage yards), Hill considered given a set of
storage yards), Hill considered given a set of ![]() points and wondered about the smallest possible number of crossings when joining by curves every pair of those points. In mathematical terms, the brick factory problem deals with the bipartite graph
points and wondered about the smallest possible number of crossings when joining by curves every pair of those points. In mathematical terms, the brick factory problem deals with the bipartite graph ![]() , while this crossing-number problem deals with the complete graph
, while this crossing-number problem deals with the complete graph ![]() .
.
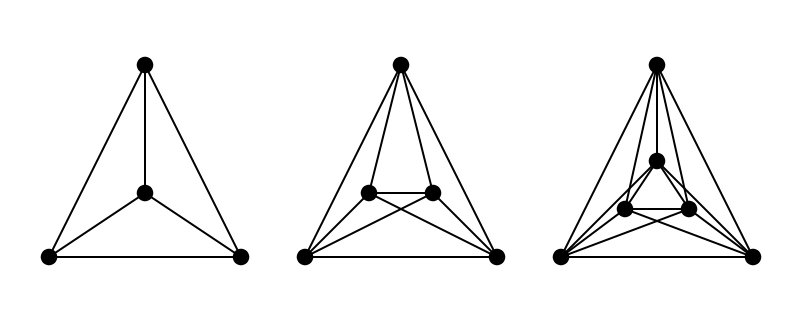
Figure 1 shows drawings of ![]() for
for ![]() having, respectively, 0, 1, and 3 crossings. Indeed, it can be proved that there is no drawing with fewer crossings, so for those graphs the crossing number, denoted as
having, respectively, 0, 1, and 3 crossings. Indeed, it can be proved that there is no drawing with fewer crossings, so for those graphs the crossing number, denoted as ![]() and defined as the smallest number of crossings in any possible drawing, is actually
and defined as the smallest number of crossings in any possible drawing, is actually ![]() ,
, ![]() , and
, and ![]() . Furthermore, observe that in those drawings the curves which join the vertices are actually straight-line segments. Such an extra condition leads to a different problem, interesting on its own.
. Furthermore, observe that in those drawings the curves which join the vertices are actually straight-line segments. Such an extra condition leads to a different problem, interesting on its own.
The problem of finding the crossing number of the complete graph has a more fuzzy history than its bipartite counterpart. It is such a natural question that several people might have attacked it before giving up, discouraged by its difficulty. In particular, Paul Erdős claimed in 1960 that he had already been thinking on the problem for at least 20 years (which might sound a bit strange, since he was well known for spreading open problems).
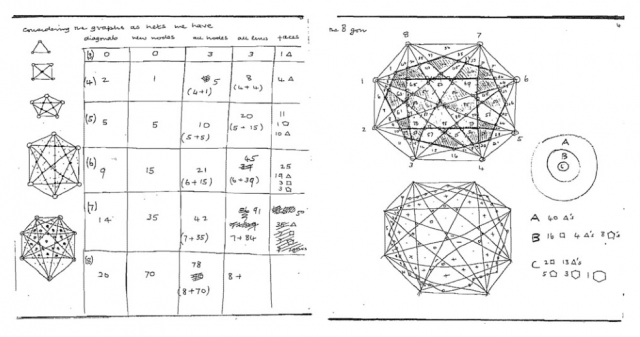
According to several unpublished notes and correspondence, it seems that the first serious investigations on the problem are due to Hill, around 1958. After consulting some colleagues about whether the problem was known, Hill performed a great deal of experimentation which allowed him to find drawings of ![]() with 3 crossings (like the one in Figure 1), of
with 3 crossings (like the one in Figure 1), of ![]() with 9 crossings, of
with 9 crossings, of ![]() with 18 crossings, and of
with 18 crossings, and of ![]() with 36 crossings. Figure 2 shows part of Hill’s notes.
with 36 crossings. Figure 2 shows part of Hill’s notes.
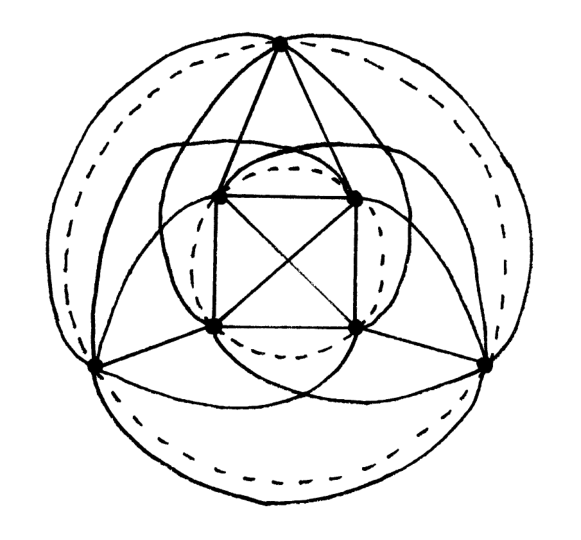
His idea was looking at diagonals of polygons, some inside and some outside. This can be checked in Figure 3, which shows Hill’s construction for ![]() with the vertices placed on two dashed circles (note that the edges in this case are actually curves).
with the vertices placed on two dashed circles (note that the edges in this case are actually curves).
Such an idea led Hill to state, in the late 1950s, which is probably the first conjecture for the crossing number of the complete graph, with two cases according to the parity of ![]() . Those two cases were later combined into a single formula by J. Blažek and M. Koman 2, who in addition proved Hill’s conjectured value to be actually an upper bound for the crossing number of the complete graph:
. Those two cases were later combined into a single formula by J. Blažek and M. Koman 2, who in addition proved Hill’s conjectured value to be actually an upper bound for the crossing number of the complete graph:
![]() .
.
By the spring of 1959, Hill and his friend the American artist John Ernest had arrived at the above conjecture and approached some professional mathematicians about the problem. One of them suggested contacting Andrew Booth at Birkbeck College, University of London, who was a computer pioneer in the 1940s. In May 1961, H. P. Goodman, a student of Booth’s, wrote a letter to Nature 3 describing their attempts to solve this seemingly intractable problem using a computer:
This problem does not appear tractable analytically, so it was programmed for the University of London Mercury computer. The programme was written on the assumption that a minimum for n+1 points can be obtained by adding an extra point in a suitable place on a minimum solution [with m crossings] for n points. However, the computations have proved that this apparently natural assumption is false: Two different minimum configurations for n=7, m=9 were taken, and one led to the true minimum n=8, m=18, while the other led to n=8, m=19.
By December 1960, their computer had yielded the values of 60 for n=10 and 100 for n=11, results that were later been proved correct.
Hill had already communicated the problem to Proffessor Ambrose Rogers, from University College, when Richard Guy gave a seminar there in November 1959, attended by Hill. Hearing about the complete graph problem, probably via Rogers, Guy published the first paper on it4 in 1960. Around this time, Hill communicated his results to the graph-theorist Frank Harary, with whom he wrote a paper5 summarizing the progress on the problem.
But it was also Guy who, in a later paper6, proved that the conjecture does provide the right crossing numbers for ![]() . Actually, the conjecture is known both as the Harary-Hill conjecture or as Guy’s conjecture. Since then, 47 years were needed until Pan and Richter7 in 2007 extended the validity of the conjecture to
. Actually, the conjecture is known both as the Harary-Hill conjecture or as Guy’s conjecture. Since then, 47 years were needed until Pan and Richter7 in 2007 extended the validity of the conjecture to ![]()

which is the current status of the crossing-number problem for the complete graph. Nevertheless, very recent results8 seem to have settled some particular cases and might have opened a door towards the resolution of the problem.
References
- Beineke L. & Wilson R. (2010). The Early History of the Brick Factory Problem, The Mathematical Intelligencer, 32 (2) 41-48. DOI: 10.1007/s00283-009-9120-4 ↩
- J. Blažek and M. Koman. A minimal problem concerning complete plane graphs, In: Theory of Graphs and Its Applications (ed. M. Fiedler), Czechoslovak Academy of Sciences (1964), 113–117. ↩
- H. P. Goodman. The complete n-point graph, Letter to Nature,190, No. 4778 (27 May 1961), 840. ↩
- Richard K. Guy. A combinatorial problem, Nabla (Bull. Malayan Math. Soc.) 7 (1960), 68–72. ↩
- Frank Harary and Anthony Hill. On the number of crossings in a complete graph, Proc. Edinb. Math. Soc. (II) 13 (1962–63), 333–338. ↩
- Richard K. Guy. Crossing Numbers of Graphs. In: Graph Theory and Applications: Proceedings of the Conference at Western Michigan University, Kalamazoo, Mich., May 10-13, 1972 (Ed. Y. Alavi, D. R. Lick, and A. T. White). New York: Springer-Verlag, pp. 111-124, 1972. ↩
- Shengjun Pan and R. Bruce Richter. The crossing number of
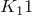 is 100, J. Graph Theory 56 (2007), 128–134. http://dx.doi.org/10.1002/jgt.20249. ↩
is 100, J. Graph Theory 56 (2007), 128–134. http://dx.doi.org/10.1002/jgt.20249. ↩ - Bernardo M. Ábrego, Oswin Aichholzer, Silvia Fernández-Merchant, Pedro Ramos & Gelasio Salazar (2013). Shellable drawings and the cylindrical crossing number of
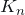 , arXiv: 1309.3665v2 ↩
, arXiv: 1309.3665v2 ↩
2 comments
[…] from the early 60s, Hill contributed papers to mathematical journals and at worldwide conferences. Hill’s Conjecture, stated in a 1963 paper co-authored with the mathematician Frank Harary, involved the variety of crossings in a whole graph; it’s nonetheless not […]
[…] from the early 60s, Hill contributed papers to mathematical journals and at worldwide conferences. Hill’s Conjecture, stated in a 1963 paper co-authored with the mathematician Frank Harary, involved the variety of crossings in an entire graph; it’s nonetheless not […]