The theory on how to ride your bike
Bikes are becoming a much more interesting mean of transport in urban areas due to the local policies to minimize traffic impact on the daily city life. City councils are building bike lanes, converting streets to mixed pedestrian-bike traffic, and similar solutions for encouraging the use of this clean mean of transport. However, this comes to a cost: while deaths in every other mean of transport decrease over the years, bike accidents remain constant, with an increasing number of serious injuries; also 80% of them have only one vehicle involved, i.e. the bike loses balance and falls with catastrophic consequences. The main reason for this is that more and more elderly people take the bike: 75% of these deaths are people over 60 years. And the fact is that, until the last few years, we had not fully understood what is what makes a bike stable and how to improve it. Schwab & Meijaard 1 have made an extensive review on bike dynamics, which includes most of their latest papers on the matter.
First, let’s make an imaginary exercise. Just take a bike, hold it vertical, and release it. If you have a bike which you don’t mind ends up scratched, you can try it in real life too. It seems rather obvious that the bike will just fall sidewise: a static bike is unstable. Now look at the following video:
At certain speed, the bike is stable without rider control(self-stable), for a long period, until the speed is reduced enough to make it unstable again. Stability means that you can perturb the system, and it will eventually go back to the stable position:
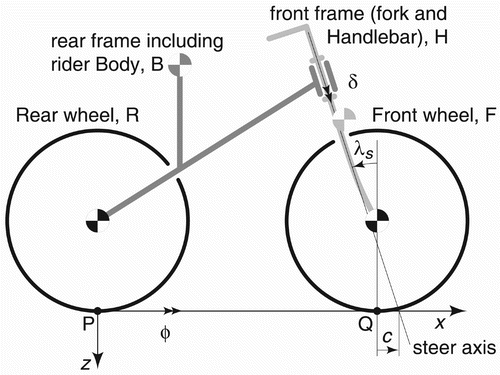
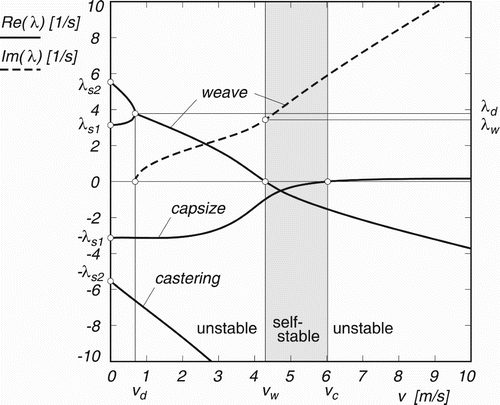
When the bike is theoretically analysed as a rigid multibody system (Figure 1), it can be seen that for a specific range of riding speeds all the eigenvalues of the system have negative real part (Figure 2). This means that every displacement combination of the different degrees of freedom of the system will have damped amplitude with time, thus making the bike stable. For lower speeds it falls down with a weaving mode (a combination of both roll and steer), which is the most common falling for conventional bike riders. For higher speeds, however, the dominant unstable mode is the capsizing mode, where the roll angle is most important, generating a spiral of decreasing radius until the bike falls. The real part of this mode is very close to zero, so it means that it’s very easy for a rider to control it and avoid the instability. For the case of low speed instability, the value of the positive root increases constantly when decreasing speed, meaning that it becomes harder and harder for the rider to control the bike when the speed gets close to zero, as most of us have experienced with our own bicycles.
When a rider controls the bike, he or she can only control one degree of freedom: the steering angle of the front wheel. So for every case, the bike is controlled by steering: when the bike falls to the left, the rider steers to the left, changing the contact point direction and generating lateral forces at the wheel-road contact that will centre the bike again. This mechanism is called “steer into the fall”, and we can even see it when the bike is running with a self-stable speed and laterally perturbed, as the bike itself steers into the fall and recovers its equilibrium.
So, what is the reason for being self-stable at certain speed? There are two groups of people that defend two different theories: the ones that think that stabilization is caused by the gyroscopic effect of the wheels; and the ones that think that stability is generated by the caster effect of the front wheel. But is the discussion still on-going? Is any of them right?
Gyroscopic effect
The gyroscopic effect is a very interesting property of rotating elements that allows fast spinning objects to maintain their spinning direction in space. Thus, the wheels of the bike tend to maintain their equilibrium position. Except that they do not; or at least the gyroscopic effect is not enough. In order to prove this, they tried to lock the steering axis. This way, if the gyroscopic effect is enough to keep it stable, the bike should stay put at these speeds. The result is that it falls down as fast as a static bike:
However, there is another interesting effect concerning gyros: if the axis of the rotating element is tilted around a second axis, an angle appears in the third (orthogonal) axis so the angular momentum is kept constant. This means that when the bike wheel leans to the left, the gyroscopic effect will steer the wheel to the left, and as we have stated, steer to the fall is the proper way of stabilizing the bicycle. Even though, this is not the only stabilizing mechanism, as you can build a bike with no angular inertia and still make it stable:
Castering
Castering is a self-guidance mechanism generated when the guidance axis is placed in front of the rolling contact point. Most supermarket strollers have castering wheels: it doesn’t matter where you go, the wheel always faces the direction of motion. In this case, when the bike leans to one side, the geometry of the castering wheel will make it steer in the same direction. This steering into the fall will equilibrate the bike again. However, you can also design a bike with no caster that is self-stable: the prototype in the previous video has also zero caster effect. The authors published their results in Science in 2011 2.
So bike stability is still not as simple as it seems. There are several mechanisms, all of them contributing slightly to the overall stability of the bicycle, but none of them is really necessary: a right mass division and positioning with the right steering axis will give a perfectly stable bike. In this specific case, the rear frame mass is very high in the front, and the mass of the steered section is in front of the steering axis. This causes that, when a roll angle appears, the rear frame will fall faster because of the higher mass; but because they are connected, it will drag the front section making it steer in the correct direction.
In a common bike, the list of parameters that can be analysed is huge. Actually, the bike model in Figure 1 is extremely simplified in order to focus in the most characteristic parameters of a common bike. Anyhow, tampering with the non-considered parameters will of course allow even more combinations of self-stable bike geometries.
Now, these studies can be very useful in many ways. The first one is that there are new types of bikes out there with different geometries, e.g. the latest bike rental systems in big cities have bikes with very low centres of gravity and smaller wheels; and these are not usually so easy to ride. A parametric study of the different components of the bike could definitely improve their performance. Foldable bikes are another weird-geometry example that could benefit from these analyses.
Another interesting point about pneumatic safety bikes is that, for a negative speed, they are unstable for every condition, meaning that if you try to ride a bike backwards you will have a very hard time.
Tampering with the different parameters can give you a rear steering self-stable bike, as the authors actually managed in their lab. Honestly, I can’t understand the advantages of rear steering, so I cannot see any usefulness to this point. It’s still interesting from a theoretical point of view, though.
And what about a system that actively controls the steering so the bike doesn’t fall? A built-in mechanism that actively controls the tilt angle of the bike acting upon the steering degree of freedom would be very useful to avoid the single-vehicle accidents that were mentioned in the first paragraph. The control system is actually very easy to build:
Integrating this on a conventional bike would allow an amazing degree of stability, reducing self-accidents to virtually zero. The system would need some electric actuators though, so if we are on it, we could just include also an electric bike motor. This would definitely be one of the most useful and environmentally friendly single-person vehicles for urban areas.
References
- Schwab A.L. & Meijaard J.P. (2013). A review on bicycle dynamics and rider control, Vehicle System Dynamics, 51 (7) 1059-1090. DOI: 10.1080/00423114.2013.793365 ↩
- J.D.G. Kooijman, J.P. Meijaard, J.P. Papadopoulos, A. Ruina, and A.L. Schwab (2011): A bicycle can be self-stable without gyroscopic or caster effects, Science 332, pp. 339–342. ↩

3 comments
[…] Esta es una traducción de un artículo que publiqué originalmente en Mapping Ignorance el 16-10-2013 – The theory on how to ride your bike. […]
The two schools of thought that I see are those that incorrectly investigate stability with the Whipple model and those like Sharp who include two more degrees of freedom and tire slip. As slip angles are the key to bike stability you need to read carefully any paper out there. For a look at why bicycles are stable see: https://www.youtube.com/watch?v=pj1bRXOHkLQ
A lot of confusion over a simple servo mechanism. When a bike tends to fall to the left[ for example], this causes the front wheel to steer to the left. It steers to the left for a number of reasons. One small effect is the gyroscopic effect which automatically applies a torque to the steer axis to steer into the fall. The other effects are caused by the castoring action of any wheel with a pneumatic trail which again will tend to cause the front wheel to steer into the fall. This is well understood and there should be no confusion except when Cornell University try to make a name for themselves with irrelevant research.
When the front wheel automatically steers into the fall left, this sets the bike on a momentary path to the left. This path to the left creates centrifugal force[ right] on the vehicle which being a STV with zero roll stability causes the vehicle to tilt back to the vertical.
So, the servo mechanism is created by the small steer torque creating a substantial roll torque in the opposite direction and the vehicle is thus fundamentally stable due to these effects.
As long as the rider holds the bars with a resilient grasp the vehicle can remain” self stable”. If the rider positions the bars the stability is destroyed and the bike will fall over. How more simple does it need to be? P.