Measuring the reality of the wavefunction

Quantum mechanics represented a revolution in physics with implications in many other fields like chemistry and biology. It also conducted changes on some of the main scientific lines of thought, including a farewell to determinism. In the science before quantum mechanics probability was accepted only as a lack of knowledge from the system being studied, but in quantum mechanics uncertainty is an inherent property of systems. In the core of this uncertainty, we find the quantum wavefunction, a mathematical entity that describes the time evolution of quantum systems and the probability of the different outcomes of any measurement. Yet the nature of the wavefunction is still unclear. Is it a physical entity with direct correspondence with an underlying reality or it just represent our limited knowledge abut a concrete system?

If wavefunctions are physical entities the measurement process involves a real change on the system. This process is called the wavefunction collapse, and its mechanics is still not well understood. This represents an ontological interpretation of quantum mechanics. Otherwise, the wavefunction can be only our knowledge about the system state and the measurement possible outcomes. From this point of view, the measurement process does not involve any collapse, as it is just an update of our information. This is the epistemological interpretation of quantum mechanics.

This kind of question belongs more to philosophy than to science, but if we mathematically define concepts as ‘reality’ or ‘knowledge’ the discussion can be transformed into experiments. In this direction, there is a huge effort to put some light into this topic and to realize what the wavefunction really is. Of course, definitions can be controversial and theorems require further assumptions, but the transformation of a philosophical matter into science never comes without a cost.

In the last few years, some theorems have been proposed. A milestone in this direction was presented in Reference ¹. In this paper, the authors proved what is called a no-go theorem. It reads: “if the quantum state merely represents information about the real physical state of a system, then experimental predictions are obtained that contradict those of quantum theory”. This result relies on two assumptions. First, for any isolated quantum system there is a ‘real physical state’. Second, systems prepared independently have independent physical states.

Let start by defining what ‘real physical state’ means. To make the discussion clearer, we will use a classical analogy. The state of a classical particle can be completely specified by giving its position x and its momentum p. Hence, the set of variables (x,p) represents all possible states. Other magnitudes, like energy, can be calculated from the states. If we know the energy of a system E we have only a partial knowledge about the state, as many combinations of (x,p) correspond to the same energy. Given a fix energy E we can only calculate a probability distribution function of the different physical states η_E(x,p). It is clear that η_E(x,p) does not represent a real state, but our state of knowledge.

In an epistemological approach to quantum mechanics, the wavefunction Ψ has a similar role than energy in the previous example. It is assumed that there is a physical real state λ and that the wavefunction Ψ corresponds to a probability distribution η_Ψ(λ). The key of the theorem lies in the following argument. As energy is a well-defined physical property the probability distribution corresponding to different energy values do not overlap. This means that for two different values of the energy there cannot be a value of the state (x,p) that corresponds to both of them. The same happens with the wavefunction. If the wavefunction corresponds to a real physical property the probability distribution of different wavefunction should not overlap. This is represented in Figure 1.

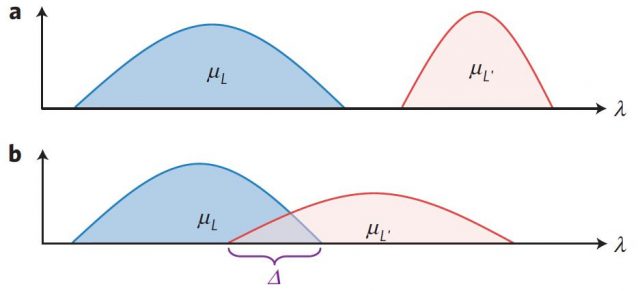
The theorem from Ref [1] states that if the probability distributions associated to different wavefunctions overlap there is a contradiction with the predictions of quantum mechanics. This means that the wavefunction should correspond to a real physical property. Even if there is an underlying physical reality it has a direct correspondence with the wavefunction.

The main problem with this result is that it relies on a strong assumption: that systems prepared independently have independent physical states. This could be considered a natural assumption, but in a non-local theory as quantum mechanics it is too strong. Furthermore, it has been proved that this assumption is necessary not only for this theorem but also for any similar no-go theorem ².

The interesting result and the dependence of this kind of theorems in the ‘preparation independence’ assumption has motivated new attempts to analyze the matter without such a strong assumption. In ³ a new experiment in this direction was performed. This experiment is based in a basic property derived from quantum physics, the non-distinguishability of different wavefunctions. In quantum mechanics, there are pairs of wavefunctions, called orthogonal, which can be distinguished with an arbitrary efficiency, but all the remaining pairs cannot. This is not a technical issue that can be improved by new technology but an intrinsic property of quantum systems. This property can be easily explained from the epistemological point of view. The wavefunction represents our limited knowledge of the underlying reality and different wavefunctions can correspond to the same physical state. Different wavefunctions cannot be distinguished because sometimes they are the same state. On the other hand, epistemic models should not only explain why there is no-distinguishability, but they should also give the statistical equivalent to the one predicted by quantum mechanics in this kind of experiments. By imposing this condition many epistemic models can be ruled out ⁴.

This experiment put limitations to the epistemic and ontological models that can be applied to quantum physics. The experiment was performed by single photons (see figure 2) and it does not rely on the ‘preparation independence’ assumption as previous attempts did. Of course, there are some assumptions. The main one is the ‘fair sampling’, meaning that the efficiency of the measurement devices is the same for any state, but this assumption is physically more reasonable than the previous one.

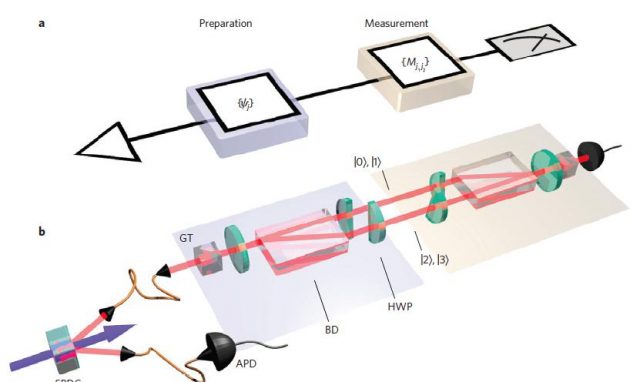
The result of the experiment rule out the possibility of fully explaining the quantum non-distinguishability by an epistemic approach. It does not rule out an epistemology approach but it clarifies that this approach should include some extra ingredients to explain this phenomenon. It also puts strong limitations to the realistic interpretations of quantum mechanics, suggesting that if we want to keep the idea of an objective reality of the wavefunction we should adopt the Bohmian pilot wave interpretation, or even the many worlds interpretation.