Increasing superconducting critical temperature by enhancing electron-phonon coupling
Topology has been at the forefront of condensed matter physics for the past two decades, influencing our understanding of quantum materials and phenomena. More recently, it has however become clear that a more general concept, that of quantum geometry, manifests itself in a series of quantum phenomena involving flat electronic bands. In condensed matter physics, the band structure of materials describes the energy levels available to electrons in a crystal lattice. Quantum geometry influences the band structure by affecting the spatial extent and shape of electron wavefunctions within the lattice.
Nontrivial quantum geometry — expressing change in wavefunctions under infinitesimal change in the Hamiltonian parameters such as momentum— appears naturally in multi-band systems. If a band is topologically nontrivial, the quantum metric is bounded from below by the topological invariant of the band. However, even if the band is topologically trivial, but has Wannier states that are not fully localized on the atoms (such as in the obstructed atomic limits), the quantum geometry — usually described up to now by the Fubini Study metric (FSM)— can be bounded from below.
For flat electronic bands — whose flatness comes from quantum interference effects — it has been shown that the quantum geometry is directly related to superfluid weight and other phenomena (such as the fractional Chern insulators, etc), mostly within contrived special models. Hence, flat bands, previously thought to be detrimental to superconductivity, actually have superfluid weight bound from below if topological. Experimental investigations of these predictions are ongoing in systems such as magic-angle twisted bilayer graphene.
Up to now, all the works on quantum geometry either do not include the realistic interaction or treat the interaction strength as a tuning parameter. Actually, it is unknown how quantum geometry affects the strength of realistic interactions. One main and important of these interactions in solids is the electron-phonon coupling, which is crucial for superconductivity and other quantum phases. As for phonon-mediated superconductors, a large electron-phonon coupling constant, which tells the strength of the coupling, typically leads to a high superconducting transition temperature, it is natural to ask how this constant is directly related to the electron band geometry which is bounded by topology. Such relation, if revealed, may help look for new superconductors, given the large number of known topological materials.
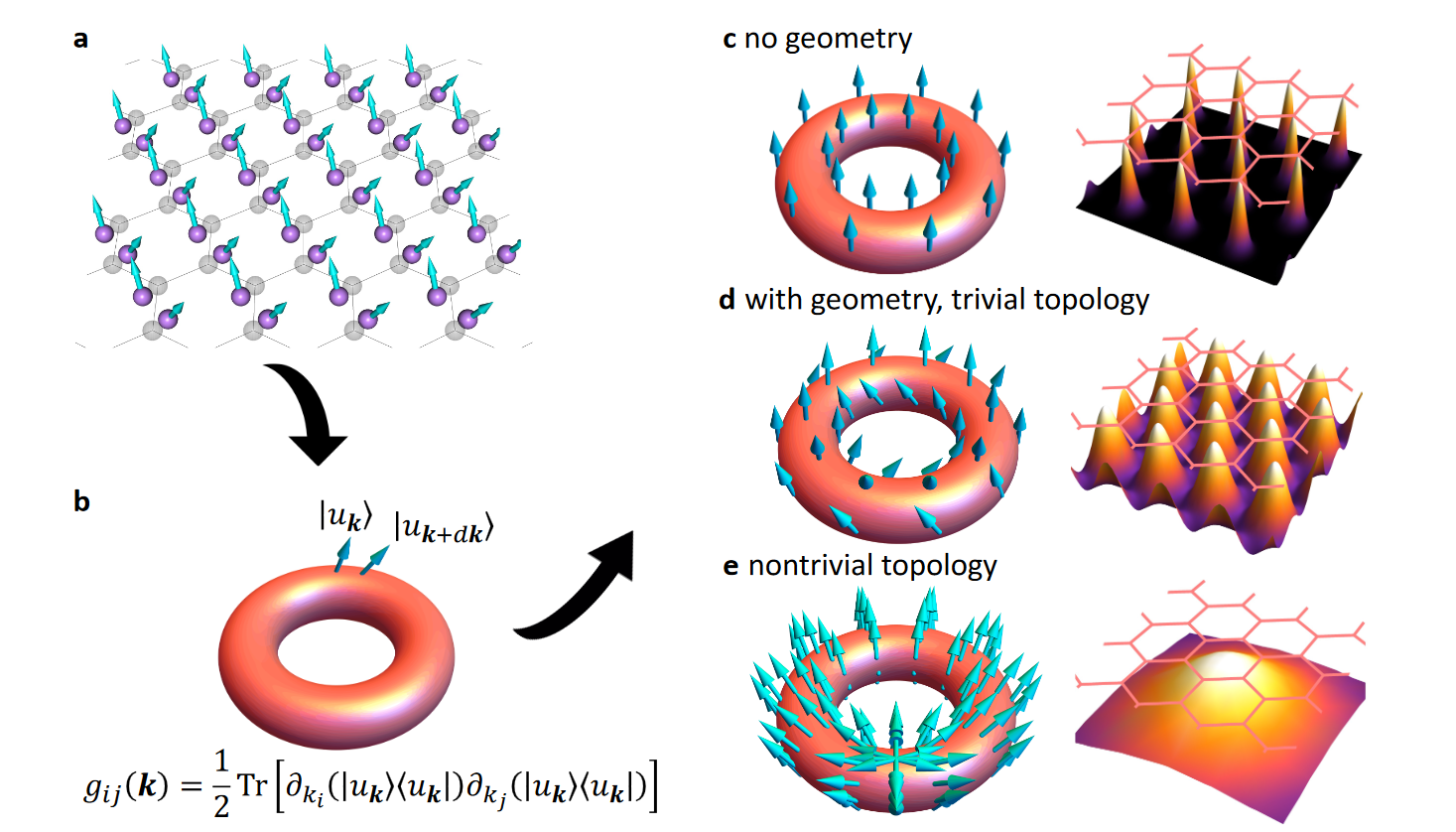
Now, a team of researchers computes 1 the contribution of electron band geometry and topology to the bulk electron-phonon constant. The team built their model by using Gaussian approximation. This method simplifies complex interactions (such as those between electrons and phonons) by approximating the distribution of variables like energies as Gaussian (or normal) distributions.
The scientists found that the overlapping was affected by the quantum geometry of the electronic wavefunction, thus affecting electron hopping. Electron hopping is a phenomenon in crystal lattices where electrons move from one site to another. For hopping to occur effectively, the wavefunctions of electrons at neighbouring sites must overlap, allowing electrons to tunnel through the potential barriers between sites. The researchers quantified this by measuring the electron-phonon coupling constant using the Gaussian approximation.
To test their theory, they applied it to two materials, graphene and magnesium diboride (MgB2). The researchers chose to test their theory on graphene and MgB2 because both materials have superconducting properties driven by electron-phonon coupling.
They found that for both materials, the coupling was strongly influenced by geometric contributions. Specifically, the geometric contributions were measured to be 50% and 90% for graphene and MgB2, respectively. They also found the existence of a lower bound or limit for the contributions due to quantum geometry.
This work suggests that increasing superconducting critical temperature, which is the temperature below which superconductivity is observed, can be done by enhancing electron-phonon coupling.
Author: César Tomé López is a science writer and the editor of Mapping Ignorance
Disclaimer: Parts of this article may have been copied verbatim or almost verbatim from the referenced research paper/s.
References
- Yu, J., Ciccarino, C.J., Bianco, R., Errea, I., Narang, P. & Bernevig, B.A. (2024) Non-trivial quantum geometry and the strength of electron–phonon coupling. Nat. Phys. doi: 10.1038/s41567-024-02486-0 ↩