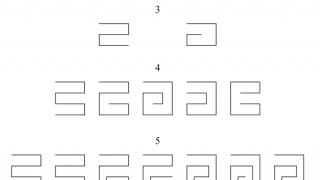
Helping Spider-Man to plan his moves efficiently
We all know how Spider-Man moves through the city, shooting spider-webs from wall to wall. But, have you ever wondered if he is actually using the shortest route? And, if so, how does he compute it? Since walls introduce a third dimension into the problem, the algorithms in a usual GPS navigator are no longer […]